质点运动学
质点运动学
运动:物体各点部位的位置随时间变化
空间
绝对空间观:
存在着没有物体(物质)的空间,物体(物质)存在并运动于该空间中,空间的内在性质(三维欧几里得性质,平直的)与物体(物质)的存在、运动与否无关。
相对论空间观:
设想或讨论不存在物体(物质)的空间是没有意义的。
真实空间是物体(物质)延展而成而且物体运动所在的空间。
真是空间的度量性质随着测量者(其载体是物体/物质)而异。
时间
绝对时间观:
存在着没有事物演化的时间流逝,事物演化于该时间流逝中。时间流逝的内在性质与事物的存在,以及演化的出现与否无关。
相对论时间观:
设想或者讨论,不存在事物演化的时间是没有意义的。
真实的时间是事物演化表现的时间。
真实时间的度量随测量者而异。
参考系
参考物
物体始终处于相对运动状态之中,最基本的运动关系或者运动内容便是两个物体之间的相对运动。
参考空间
参考物在体结构上静态延展而成的三维平直空间(在宏观世界里)
空间坐标系
来标定空间
时间坐标
来标定时间
质点
物体各个小部位模型化为质点。
如果物体中各个小部位运动相同的时候(平动),可以把物体整体模型化为一个质点。
物体当中各个小部位运动情况虽然不同,但其间差异相对所考察的运动线度可以忽略,可以把物体整体模型化为一个质点。
直线运动
位移
x=x(t)称为运动方程
\(\Delta x=x(t+\Delta t)-x(t),被标量化了,用正负号表示方向\)
无穷小位移,从t→t+dt,dx(也被标量化)
dx=x(t+dt)-x(t)
\(\Delta x=\int_{t}^{t+\Delta t}dx\)
路程
\(ds=|dx|,\Delta s=\int_{t}^{t+\Delta t}|dx|\)
速度
\(\vec{v}=\frac{\Delta \vec{x}}{\Delta t}\)
加速度
\(\vec{a}=\frac{d\vec{v}}{dt}\)
三类直线运动
匀速直线运动
a=0, v常量
匀加速
a=常量,\(v=v_0+at,x=x_0+v_0t+\frac{1}{2}at^2,v_x^{2}-v_0^{2}=2a(x-x_0)\)
变加速
范例:简谐振动 \(x=Acos(\omega t+\phi)\)
平面曲线运动
\(\vec{r}=\vec{r}(t)=x(t)\vec{i}+y(t)\vec{j}\)分解为X,Y两个方向的运动
位移\(\Delta \vec{r}=\vec{r}(t+\Delta t)-\vec{r}(t)\)
速度\(\vec{v}=\frac{d\vec{r}}{dt}=v_x \vec{i}+v_y \vec{j}\)
加速度\(\vec{a}=\frac{d\vec{v}}{dt}=a_x \vec{i}+a_y \vec{j}\)
斜抛运动
初速度\(v_0\)斜向上,与x轴夹角\(\theta\)
通过写出x,y关于t的方程可以解出来轨道方程
\(y=\frac{-g}{2v_0^{2}cos^2\theta}x^2+(tan\theta) x\)
射高:\(H=\frac{v_0^2sin^2\theta}{2g}\)
水平射程:\(s=\frac{v_0^2sin2\theta}{g}\) 给定的\(v_0\)有两个互余的锐角对应相同的s
下面我们考虑\(v_0\)给定,\(\theta\)可变,我们求解包络线的方程
包络线的数学定义: 如果一族曲线由方程 F(x,y,t)=0 表示,其中 t 是参数,那么该族曲线的包络线满足以下两个条件:
F(x,y,t)=0 (曲线本身的方程)
\(\frac{\partial F}{\partial t}=0\)
解法一 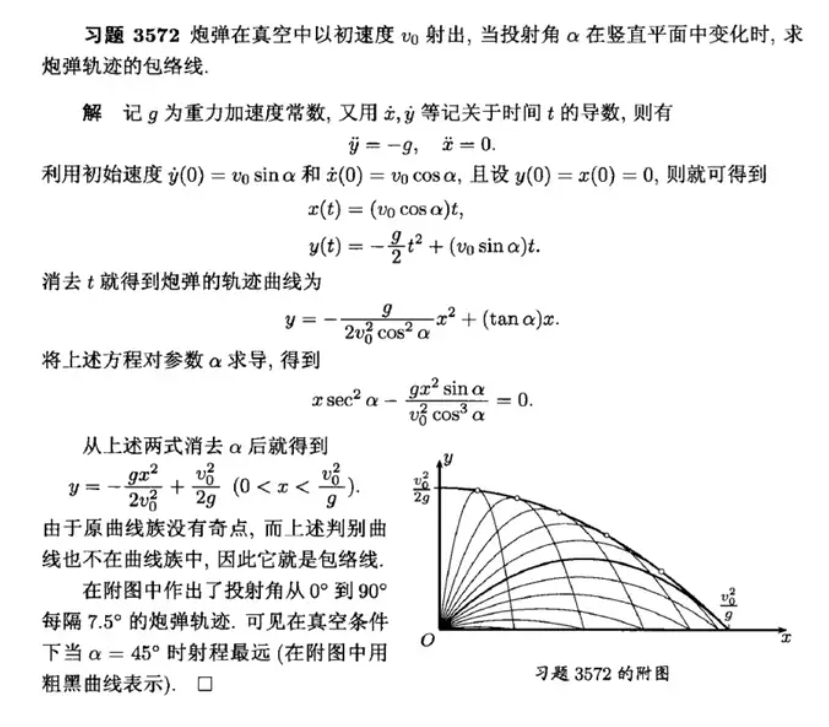
解法二 这里\(\frac{\partial F}{\partial t}=0\)意味着对于每个x,y只有一个\(\theta\)与之对应
\(tan \theta=\frac{v_0^{2}+-\sqrt{v_0^4-2v_0^2gy-g^2x^2}}{gx}\)
\(\Delta=0\)可知\(v_0^4-2v_0^2gy-g^2x^2=0\) 包络线本身也是一个数学上的抛物线
自然坐标系分解
平面曲线运动的一般特点
\(\vec{r}=x(t)\vec{i}+y(t)\vec{j}\)
如果x(t),y(t)相互独立,则称这个质点运动有两个自由度
若质点运动被约束在一条平面曲线上,则有F(x,y)=0,此时x(t)y(t)并非相互独立,此时只有一个自由度
圆周运动
\(x^2+y^2=R^2,R为不变量\)
角位移,角速度都是标量
角加速度\(\beta=\frac{d\omega}{dt}\)
线位移\(d \vec{l}=dl\vec{\tau}=Rd\theta\vec{\tau}(\vec{\tau}是切向方向向量)\)
线速度\(d \vec{v}=R\omega\vec{\tau}\)
\(d\vec{v}=d\vec{v}_心+d\vec{v}_切\)
\(d\vec{v}_心\) 方向向心,大小\(vd\theta\)
\(d\vec{v}_切 方向切向,大小dv(注意不是|d\vec{v}|)=Rd\omega\)
\(\vec{a}_心 方向向心,大小v\omega\)
\(\vec{a}_切 方向切向,大小R\beta\)
角量的矢量化
引入\(\vec{k}\)
\(\vec{d\theta}=d\theta\vec{k}\)
\(\vec{dl}=\vec{d\theta}\times\vec{r}\)
\(\vec{\omega}=\omega \vec{k}\)
\(\vec{v}=\vec{\omega}\times\vec{r}\)
\(\vec{\beta}=\frac{d\omega}{dt}\vec{k}=\beta\vec{k}\)
\(\vec{a}=\frac{d(\vec{\omega}\times\vec{r})}{dt}=\frac{d\vec{\omega}}{dt}\times\vec{r}+\vec{\omega}\times\frac{d\vec{r}}{dt}\)
注意到\(d\vec{r}=d\vec{l}\)
所以\(\vec{a}=\vec{\beta}\times\vec{r}(a_{切})+\vec{\omega}\times\vec{v}(a_{心})\)
平面光滑曲线运动的圆分解
曲率半径\(\rho\)
曲率\(k=\frac{1}{\rho}\)
\(a_心(a_n)=\frac{v^2}{\rho}\)
\(a_切(a_\tau)=\frac{dv}{dt}\)
通过物理方法来求解曲率半径\(\rho=\frac{v^2}{a_心}\)
例如:\(y=Acosx\)求顶点处的曲率半径
设:\(x=v_0t\) \(y=Acosv_0t\)
\(v_x=v_0\)
\(v_y=-v_0Asinv_0t\)
\(a_x=0\)
\(a_y=-v_0^2Acosv_0t\)
取t=0,这时\(v=v_0,a_x=0,a_y=-v_0^2A(向心加速度)代入得\rho=\frac{1}{A}\)
极坐标系分解
用极坐标表示的曲线
\(x=rcos\theta,y=rsin\theta\)
\(r=A(1-cos\theta)心脏线\)
\(r=r_0\theta阿基米德螺旋线\)
\(r=r_0e^{\frac{\theta}{\alpha}}(\alpha>0)对数螺线\)
极坐标观点下的运动学
\(\vec{e_r}径向方向矢量;\vec{e_\theta}角向(横向)方向矢量——移动的正交分解\)
运动方程\(\vec{r}=\vec{r}(t)\)
\(\vec{v}=\frac{\vec{dr}}{dt}\)
\(\vec{r}=r\vec{e_r}\)
\(\vec{de_r}=d\theta\vec{e_\theta}\)
\(\vec{de_\theta}=-d\theta\vec{e_r}注意负号!\)
\(\vec{v}=\frac{dr}{dt}\vec{e_r}+r\frac{\vec{de_r}}{dt}=\frac{dr}{dt}\vec{e_r}+r\frac{d\theta}{dt}\vec{e_\theta}\)
\(\vec{v}=v_r\vec{e_r}+v_\theta\vec{e_\theta}\)
\(v_r=\frac{dr}{dt};v_\theta=r\frac{d\theta}{dt}\)
\(\vec{a}=\{\frac{d^2r}{dt^2}-r(\frac{d\theta}{dt})^2\}\vec{e_r}+\{r\frac{d^2\theta}{dt^2}+2\frac{dr}{dt}\frac{d\theta}{dt}\}\vec{e_\theta}\)
\(径向加速度a_r=\frac{d^2r}{dt^2}-r(\frac{d\theta}{dt})^2\)
\(角向加速度a_\theta=r\frac{d^2\theta}{dt^2}+2\frac{dr}{dt}\frac{d\theta}{dt}(第二项是科里奥利加速度)\)
平面曲线的运动轨道
\(r=r(\theta)\)
\(r=r(t),\theta=\theta(t)联立把t消掉可以得到r(\theta)\)
\(v_r=\frac{dr}{dt};v_\theta=r\frac{d\theta}{dt}\)
\(\frac{dr}{d\theta}=r\frac{v_r}{v_\theta}\)
\(若已知v_r,v_\theta与r和\theta的表达式,可以推出r(\theta)。这种方式多见于天体运动种的推导\)
空间曲线运动
质点的空间运动
运动方程:\(\vec{r}(t)=x(t)\vec{i}+y(t)\vec{j}+z(t)\vec{k}\)
\(\vec{v}=v_x\vec{i}+v_y\vec{j}+v_z\vec{k}\)
\(\vec{a}=a_x\vec{i}+a_y\vec{j}+a_z\vec{k}\)
质点系和刚性质点系
质点系
定义:由若干质点构成的系统
自由度
取出第i个质点,运动不受约束,它的运动方程\(\vec{r_i}(t)=x_i(t)\vec{i}+y_i(t)\vec{j}+z_i(t)\vec{k}\)。有三个独立坐标,称为有三个运动自由度。
N个质点构成 质点系,各个质点的运动都不受约束,那么有3N个自由度。
刚性质点系
定义:每两个质点的间距不变。
自由度
取出三个不共线的质点,那么可以唯一确定一个平面。命名为1,2,3号质点。如果\(\vec{r_1},\vec{r_2},\vec{r_3}\)确定,可以确定整个系统所有点的位置。此时自由度取决于1,2,3.
1,2,3还有三个约束方程(来刻画距离不变)
因此刚性质点系运动的参量只有6个。
运动分解
平动+转动
平动有三个自由度;转动有三个自由度
参考系间的相对运动
参考系间平动
在S系,\(\vec{r}(t)\);在S'系,\(\vec{r}(t)\);刻画O'相对S系运动\(\vec{r_{O'}(t)}\)
伽利略变换:
\(\vec{r}(t)=\vec{r_{O'}(t)+\vec{r'}(t)}\)
\(\vec{v}(t)=\vec{v_{O'}}(t)+\vec{v'}(t)\)
\(\vec{a}(t)=\vec{a_{O'}}(t)+\vec{a'}(t)\)
参考系间的匀速定轴转动
例子:地球参考系相对于地心参考系做匀速定轴转动
参考系中质点间的相对运动
某参考系如果有两个运动质点A,B。建立一个随A一起相对S系运动(平动)的参考系,称之为平动参考系A系,便可以描述B在A系中的运动。这个运动就是在背景参考系S中B相对A的运动。
例子:滚轮线运动
习题
题1
长(L)的均匀弹性绳(AB)自由伸直地放在光滑水平桌面上,绳的(A)端固定。(t = 0)时,一小虫开始从(A)端出发以相对绳的匀速度(u)在绳上朝(B)端爬去,同时绳的(B)端以匀速度(v)沿绳伸长方向运动,试求小虫爬到(B)端的时间(T)。
解答: 这道题目求解的难点在于,绳子的长度随着时间的变化而变化,所以我们不方便对绳子的真实长度直接做讨论。
因此我们引入一个(相对于绳子)的坐标系,即便绳子的真实长度改变了,我们依旧把它看作L。在这种坐标系之下,设小虫子的坐标为x。
那么小虫子的真实坐标\(x'=x\frac{L+vt}{L}\)
因此,\(dx'=\frac{L+vt}{L}dx\) 注意到\(dx'=udt\)
于是我们可以把dx'替换为dx,即\(dx=\frac{L}{L+vt}udt\)
\(\int_{0}^{T} \frac{dt}{1+v\frac{t}{L}}=\int_{0}^{L}\frac{dx}{u}\)
\(T=\frac{L}{v}(e^\frac{v}{u}-1)\)
题2
一个小虫子以相对圆柱速度为u爬行,圆柱半径\(r=r_0(1+\alpha t)\)
解答:类似于题1,但有一种更简单的方式
考虑\(d\theta=\frac{udt}{r(t)}\),两边积分即可
题3
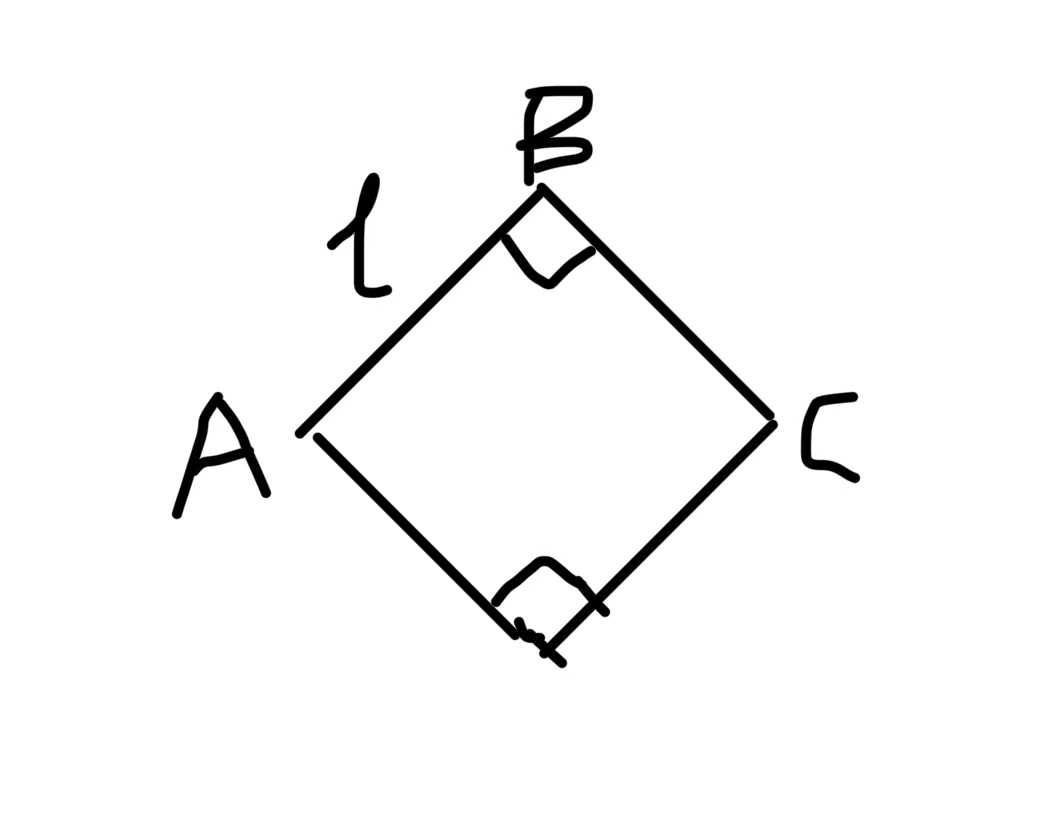
\(加速度\vec{a}速度\vec{v}\),求此时B点加速度。(A固定)
解答:这个问题我们可以用两种方式求两个加速度的分量,然后把这两个分量进行合成。
方式一:水平竖直分解
注意到B点的水平方向速度是\(\frac{1}{2}v\),水平加速度是\(\frac{1}{2}a\)
方式二:把B看作绕A的圆周运动
用圆周运动向心加速度公式求出向心加速度。
题4
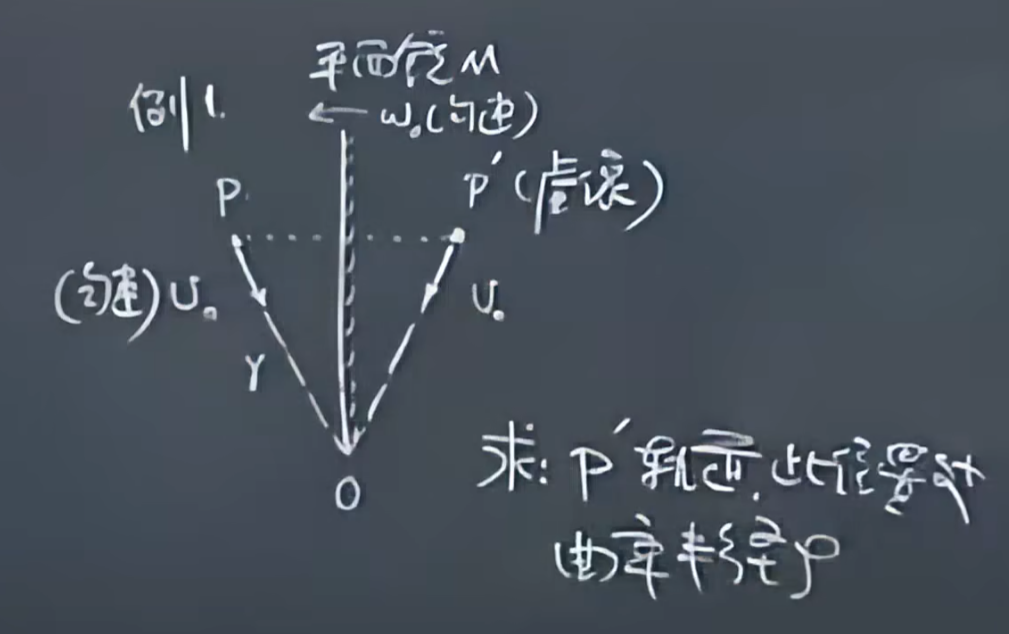
解答: \(以O为坐标系原点建立极坐标系,可以观察到\omega(P'的速度)=2\omega_0\)
\(v_r=-v_0(指向O所以是负的)\)
\(v_\theta=r\omega=2r\omega_0\)
\(a_r=0-r\omega^2=-4r\omega_0^2\)
\(a_\theta=0+2(-v_0)\omega=-4v_0\omega_0\)
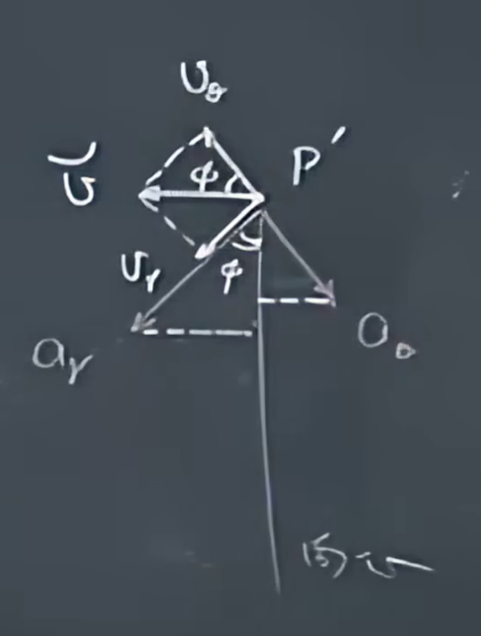
\(a_心=(4rw_0^2)cos\phi+(4v_0\omega_0)sin\phi\)
\(cos\phi=\frac{2r\omega_0}{v};sin\phi=\frac{v_0}{v}\)
\(v=\sqrt{v_0^2+4r^2\omega_0^2}\)
\(\rho=\frac{v^2}{a_心}\)
\(\rho=\frac{(v_0^2+4r^2w_0^2)^\frac{3}{2}}{4\omega_0(v_0^2+2r^2\omega_0^2)}\)
题5
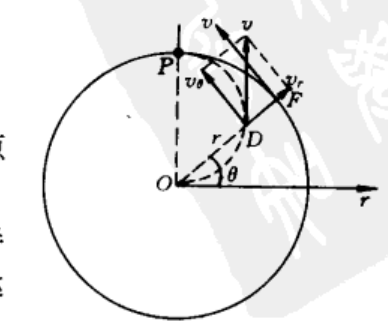
狐狸沿半径R的圆轨道以恒定速率v奔跑,在狐狸出发的同时,猎犬从圆心出发以相同的速率v追击过程中,圆心、猎犬和狐狸始终连成一直线。取圆心O为坐标原点,从O到狐狸初始位置设置极轴,建立极坐标系。
导出猎犬\(v_r,a_r,a_\theta\)与猎犬所在位置参量\(r,\theta\)间的关系;
确定猎犬运动轨道的极坐标方程,并画出轨道曲线;
判断猎犬能否追上狐狸?
解答: 对猎犬分析:因为共线,\(v_\theta=r\omega=\frac{r}{R}v,v_r=\sqrt{v^2-v_0^2}\)
\(\frac{dr}{d\theta}=r\frac{v_r}{v_\theta}=\sqrt{R^2-r^2}\)
\(\int_{0}^{r}\frac{dr}{\sqrt{R^2-r^2}}=\int_{0}^{\theta}d\theta\)
\(arcsin\frac{r}{R}=\theta或者r=Rsin\theta(圆)\)
二者正好在顶点相遇(走过的弧长相同)