牛顿定律与动量定理
牛顿定律
适用范围:宏观世界,低速(v<<c)
牛顿第一定律
内容:每个物体都会保持静止状态,或匀速直线运动,除非它被施加在其上的力改变这种运动状态。
惯性系:牛顿第一定律成立的参考系,否则为非惯性系
牛顿第二定律
内容:\(\vec{F}=\frac{d(m\vec{v})}{dt}\) m为不变量
或者可以写为:\(\vec{F}=m\vec{a}\) m为惯性质量,F为物体所受的外力
牛顿第三定律
相互作用力是径向力
相互作用力
基本的相互作用
万有引力相互作用
电相互作用
弱电作用
强相互作用&弱相互作用
常见的力
重力
来源于万有引力
弹力、摩擦力、浮力
来源于电作用力
力学相对性原理
在所有惯性系中,力学定律有相同的表达形式
惯性力
在惯性系中,\(F_真=ma\),但在非惯性系中并非如此
于是我们构造出\(F_虚(惯性力)\)
平动加速非惯性系S’
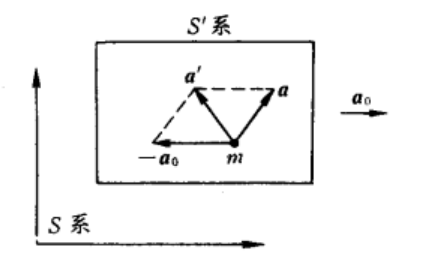
\(\vec{a'}=\vec{a}+(-\vec{a_0})\)
\(\vec{F'}=\vec{F_真}+\vec{F_惯}\)
平移惯性力\(\vec{F_惯}=-m\vec{a_0}\)
例子:类重力(考虑向前加速的车厢)
例子:潮汐现象

二体系统与约化质量
S系统由A,B构成,A、B之间有相互作用力\(\vec{F_A}\vec{F_B}\)
S系中\(\vec{F_A}+\vec{F_B}=0\) \(\vec{a_A}=\frac{\vec{F_A}}{m_A}\)
构造A系,随着A相对S系统作平动的参考系,讨论B的运动,即B相对A的运动。
\(m_B\vec{a_B'}=\vec{F_B}+m_B(-\vec{a_A})\),此时代入\(\vec{a_A}\)
得到\(m_B\vec{a_B'}=\frac{m_A+m_B}{m_A}\vec{F_B}\)
\(\vec{F_B}=\frac{m_Am_B}{m_A+m_B}\vec{a_B'}\) 类牛顿第二定律,没有惯性力
称\(\mu=\frac{m_Am_B}{m_A+m_B}\)为约化质量
惯性离心力
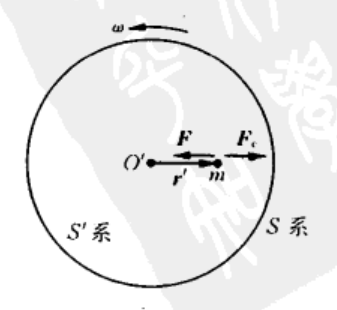
S'系是一个匀速定轴旋转的非惯性系
如果m相对S'静止,则\(\vec{a'}=0,\vec{a}=-\omega^2r\)
S系:\(\vec{F_真}=m\vec{a}=-m\omega^2r\)
S'系:\(\vec{F'}=m\vec{a'}=0\) 惯性离心力即是抵消真实力的虚拟力
\(\vec{F_c}=m\omega^2\vec{r}\)
惯性离心力是由质点在S'系的位置确定,背向圆心。
类似于胡克力,\(F_x=-kx\),\(E_p(x)=\frac{1}{2}kx^2\)
如果我们选取r=0点位“势能零点”则有\(E_p(r)=-\frac{1}{2}m\omega^2r^2\),称之为离心势能
科里奥利力
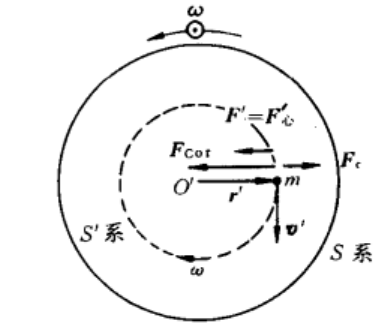
假设质点M相对S系静止 \(\vec{a}=0\)
在S’系中。m正在旋转,\(\vec{a'}=-\omega^2\vec{r}\)
S系中:\(\vec{F_真}=m\vec{a}=0\)
S'系中:\(\vec{F'}=m\vec{a'}=-m\omega^2\vec{r}=\vec{F_真}+\vec{F_c}+\vec{F_{cor}}\)
\(\vec{F_{cor}}=-2m\omega^2\vec{r}\) 方向指向圆心
科里奥利力由质点相对S’系运动而形成
改造:\(\vec{F_{cor}}=2m\vec{v'}\times\vec{\omega}\)(角速度方向用右手螺旋判断,指向纸外或者指向纸内)
因为力的方向与运动方向总是垂直的,我们可以看出科里奥利力总是不做功的,类似于洛伦兹力
实例:傅科摆验证地球自转
如果是轴向运动,因为\(\vec{v_轴}与\vec{\omega}平行\),所以此时\(\vec{F_{cor}}=0\)
动量定理
引入:\(d\vec{I}=\vec{F}dt\) 冲量元 \(\vec{P}=m\vec{v}\)
\(d\vec{I}=d\vec{P}\) 质点动量定理的微分式
\(\vec{I}=\int_{\Delta t}d\vec{I}\) 冲量
\(\vec{I}=\Delta \vec{P}\) 质点动量定理的积分式
非惯性系的质点动量定理:\(\vec{dI_真}+\vec{dI_惯}=\vec{dP}\)
质点系动量定理
质点系动量\(\vec{P}=\Sigma_{i}\vec{P_i}\)
外力提供的冲量形式等于质点系总动量增加量 \(d\vec{P}=d\vec{I_外}\)
\(\vec{F_{合外}}=\frac{d\vec{P}}{dt}\)
非惯性系的质点系动量定理\(d\vec{I_外}+d\vec{I_惯}=\vec{dP}\)
动量守恒定理
整体守恒:过程中恒有合外力为零,则过程中动量守恒
分量守恒:如果过程中恒有合外力在某一个分量上为零,则过程中有在该分量守恒
变质量物体的平动
增质型
例子:下落的雨滴
假设原来为m,受力\(\vec{F}\),速度\(\vec{v}\)
增加为dm。受力\(\vec{dF}\),速度\(\vec{v'}\)
经过dt时间二者缩合变成m+dm,速度为\(\vec{v}+\vec{dv}\)
\((\vec{F}+d\vec{F})dt=(m+dm)(\vec{v}+d\vec{v})-m\vec{v}-dm\vec{v'}\)
\(\vec{F}=m\frac{\vec{dv}}{dt}+(\vec{v}-\vec{v'})\frac{dm}{dt}\)
特例:\(\vec{v'}=0\)
则\(\vec{F}=\frac{d(m\vec{v})}{dt}\)
减质型
例子:火箭
假设原来为m,受力\(\vec{F}\),速度\(\vec{v}\)
减少量为dm(负数)受力\(\vec{dF}\),速度\(\vec{v'}\)
经过dt时间原来的物体质量变成m+dm,速度为\(\vec{v}+\vec{dv}\)
\(\vec{F}dt=(m+dm)(\vec{v}+\vec{dv})+(-dm)\vec{v'}-m\vec{v}\)
\(\vec{F}=m\frac{\vec{dv}}{dt}+(\vec{v}-\vec{v'})\frac{dm}{dt}\)(同上)
引入:分离速度\(\vec{u}=\vec{v}-\vec{v'}\)
于是\(\vec{F}=m\frac{\vec{dv}}{dt}+\vec{u}\frac{dm}{dt}\)(同上)
题目
题1
1、讨论半圆圆周轻绳中的张力分布(可以看成轻绳绕理想滑轮,无摩擦)
切向的力平衡关系\(T(\theta)cos\frac{d\theta}{2}=T(\theta+d\theta)cos\frac{d\theta}{2}\)
因此张力是一个常量
2、讨论\(n=\frac{dN}{dl}\)的大小
\(dN=T(\theta+d\theta)sin\frac{d\theta}{2}+T(\theta)sin\frac{d\theta}{2}\)
运用小量近似可以看出\(\frac{dN}{d\theta}=T\)
因此\(n=\frac{T}{R}\) 是一个常量!
题2
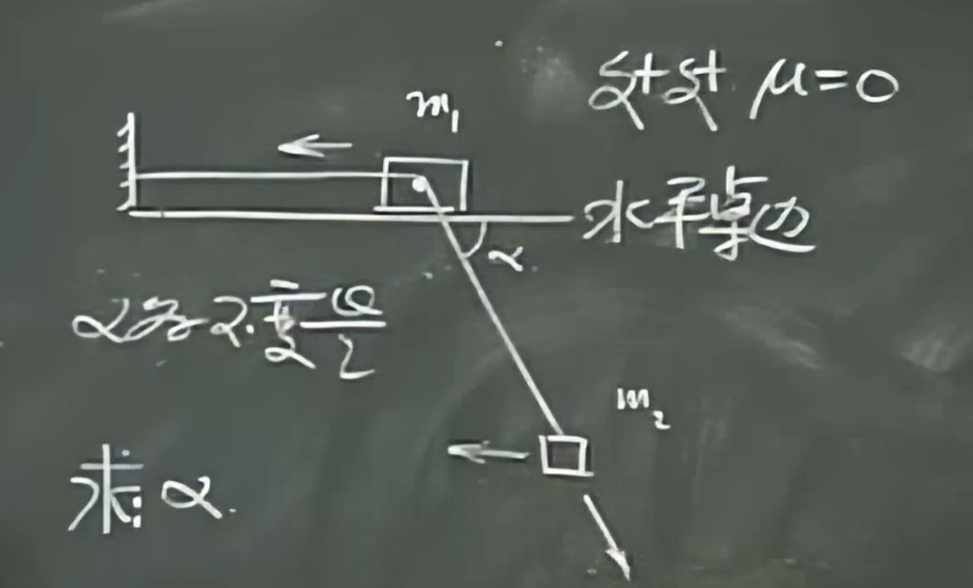
动力学方程
\(对m_1:T-Tcos\alpha=m_1a_1\)
\(对m_2:竖直方向m_2g-Tsin\alpha=m_2a_2sin\alpha\)
\(水平方向Tcos\alpha=m_2(a_1-a_2cos\alpha)\)
运动关联:\(m_2沿着绳子伸长的大小=m_1向左的大小\)
因此\(a_1=a_2\)
最终解出\(\alpha=arccos\{\frac{1}{2}(k+2-\sqrt{k(k+1)})\}\)
\(k=\frac{m_1}{m_2}\)
题3
竖直平面上有一半径(R)的固定光滑大圆环,环上套的小珠从最低处以水平初速率\(v_0\)向上运动,则可知当\(v_0\geq\sqrt{4Rg}\)时,小珠可到达环的最高点。
将一小珠套在半径(R)的水平光滑大圆环上,环绕着过其边缘点(A)的固定竖直轴以角速度()沿逆时针方向匀速旋转。开始时小珠在(A)的对径点上,沿着逆时针方向相对环以初速率\(v_0\)运动,试问\(v_0\)取何值时小珠能到达(A)点?
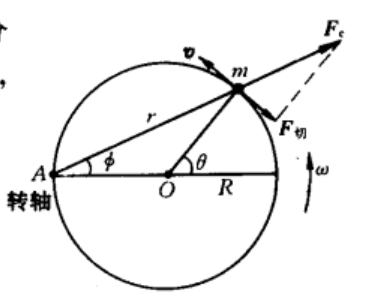
取圆环参考系,注意惯性离心力的方向!
引入惯性离心势能,注意到科里奥利力不做功
\(0+0=\frac{1}{2}mv_0^2-\frac{1}{2}m\omega^2(2R)^2\)
\(v_0\geq 2\omega R\)
题4
竖直上抛一个小球,已知空气阻力\(\vec{f}=-\gamma \vec{v}\),求过程时间t
取向上为正方向,假设初速度大小\(v_1\)末速度大小\(v_2\)
\(-mv_2-mv_1=-mgt+\int_{0}^{t_上}-\gamma v dt+\int_{t_上}^{t}\gamma v dt\)
注意到两个积分和=0
所以\(t=\frac{v_1+v_2}{g}\)
题5
质量 M 的匀质细软绳,下端恰好与水平地面接触,上端用手提住,使绳处于静止伸直状态。而后松手,绳自由下落,试求绳落下 ( l < L ) 长度段的时刻地面所受正压力大小 ( N )。
解答:
\(N_1=\frac{l}{L}Mg\)
\(v=\sqrt{2gl}\)
\(\frac{vdt}{L}Mv=N_2dt\)
\(N_2=\frac{M}{L}v^2=2\frac{l}{L}Mg\)
\(N=N_1+N_2=3\frac{l}{L}Mg\)
题6

假设虫子的初速度是\(v_m\),杆的初速度是\(v_M\)
在小虫刚开始向上爬的极短的时间内,小虫与杆构成的系统动量守恒 \(mv_m=Mv_M\)
相对速度:\(v=v_m+v_M\)
我们需要约束,小虫到容器最上面的时候,细杆顶端也到容器最上面
假设t时间段 \(\frac{L}{2}=v_Mt+\frac{1}{2}gt^2\)
\(L=vt\)

题7
火箭初始质量为\(m_0\),其中液体燃料质量\(m_l\),自地面竖直向上发射,重力加速度近似取成常量g,略去阻力。设火箭在单位时间向下喷出的液体燃料质量为\(\alpha\),喷射速度为常量\(u_0\),试求燃料喷尽时火箭的速度\(v_c\)。
解答:取向上为正方向
\(-mg=m\frac{dv}{dt}+u_0(-\alpha)\)
\(\frac{dv}{dt}=\frac{dv}{dm}\frac{dm}{dt}\)
\(\frac{dm}{dt}=-\alpha\)
\(-mg=-\alpha m\frac{dv}{dm}-\alpha u_0\)
\(\int_{0}^{v_c}dv=\int_{m_0}^{m_c}(\frac{g}{\alpha}-\frac{u_0}{m})dm\)
\(v_c=u_0ln^{\frac{m_0}{m_0-m_l}}-\frac{m_lg}{\alpha}\)