机械能定理
动能定理
功与功率
\(\vec{F}\) 做功定义为\(dw=\vec{F}\cdot\vec{dl}=Fdlcos\theta\)
功率定义:\(P=\frac{dW}{dt}=\vec{F}\cdot\vec{v}\)
重力功:W=mgh
弹力功:\(W=\frac{1}{2}k(x_1^2-x_2^2)\)
一对作用力与反作用力的做功之和是参考系不变量
\(P_1\)与\(P_2\), \(P_1\)对\(P_2\)力为\(\vec{F_1}\), \(P_2\)对\(P_1\)力为\(\vec{F_2}\), 极坐标系中\(P_1\)对应坐标为\(\vec{r_1}\). \(P_2\) 对应坐标为\(\vec{r_2}\)
\(dW=\vec{F_1}\cdot\vec{dr_1}+\vec{F_2}\cdot\vec{dr_2}=\vec{F_2}\cdot(\vec{dr_2}-\vec{dr_1})\)
\(dW=\vec{F_2}\cdot\vec{dr}\) 与相对位移有关
如果是平动参考系,显然\(\vec{dr'}=\vec{dr}\),\(dW'=dW\)证毕
考虑转动参考系
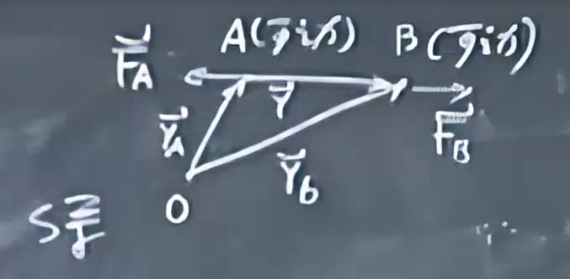
经历dt
S’系:
\(\vec{r_1'}变为\vec{r_1'}+\vec{dr_1'}\)
\(\vec{r_2'}变为\vec{r_2'}+\vec{dr_2'}\)
\(dW'=\vec{F_1}\cdot\vec{dr_1'}+\vec{F_2}\cdot\vec{dr_2'}=\vec{F_2}\cdot(\vec{dr_2'}-\vec{dr_1'})\)
S系:
\(\vec{r_1}变为\vec{r_1}+\vec{dr_1}\)
\(\vec{r_2}变为\vec{r_2}+\vec{dr_2}\)
\(\vec{d\theta}=\omega dt\)
S'相对S系转过的位移可以用\(d\theta\times\vec{r_1'}\)来刻画
\(d\vec{r_1}=d\theta\times\vec{r_1'}+d\vec{r_1'}\)
\(d\vec{r_2}=d\theta\times\vec{r_2'}+d\vec{r_2'}\)
\(dW=\vec{F_1}\cdot\vec{dr_1}+\vec{F_2}\cdot\vec{dr_2}\)
\(dW=\vec{F_2}\cdot(\vec{dr_2'}-\vec{dr_1'})+\vec{F_2}\cdot d\theta \times(\vec{dr_2'}-\vec{dr_1'})\)
混合乘积可以交换顺序(只要保证相对次序不变)
因此\(dW=\vec{F_2}\cdot(\vec{dr_2'}-\vec{dr_1'})+d\theta \cdot (\vec{dr_2'}-\vec{dr_1'})\times \vec{F_2'}\)(平行,叉乘为零)
所以\(dW=dW'\)
特例1:刚性质点系
内力做功之和一定为0
特例2:物体中接触性的内力做功之和为零
万有引力功(二体系)
假设有m,M两个对象
\(\vec{F_m}=-\frac{GMm}{r^3}\vec{r}\)
\(dW=\vec{F_m}\cdot\vec{dr}=-\frac{GMm}{r^3}\vec{r}\cdot\vec{dr}\)
因为夹角很小可以把上式近似看为:\(dW=-\frac{GMm}{r^3}rdr=-\frac{GMm}{r^2}dr\)
\(W_{ab}=\int_{\vec{r_a}}^{\vec{r_b}}-\frac{GMm}{r^2}dr=GMm(\frac{1}{r_b}-\frac{1}{r_a})\)
质点的动能定理
\(dW=\vec{F}\cdot\vec{dl}=F_切dl=ma_切dl=m\frac{dv}{dt}dl=d(\frac{1}{2}mv^2)\)
非惯性系:\(dW_惯+dW=dE_k\)
引入\(E_k=\frac{1}{2}mv^2\),于是\(dW=dE_k\)
质点系动能定理
\(E_k=\Sigma E_{k_i}\)
质点系动能定理: \(dE_k=dW_内+dW_外\)
非惯性系:\(dE_k=dW_{内}+dW_{外}+dW_{惯}\)
保守力与势能
保守力
保守力可以是真实力也可以是假想的惯性力。如果一个力的初始位置和终止位置确定,做功与路径无关的力,是保守力。如果做功与路径有关,则是非保守力。
保守力:重力、胡克弹力、万有引力
非保守力:摩擦力
\(\oint_L\vec{F}\cdot\vec{dl}=0\) 对任意闭合路径L,保守力做功为零。
作用力与反作用力保守性
初始的相对位置,终止的相对位置如果确定。
第一种情况:做功之和与其间路径无关——保守性的作用力与反作用力
第二种情况:做功之和与其间路径有关——非保守性的作用力与反作用力
这种定义与参考系无关
势能
保守力势能
\(\int_{r_a}^{r_b}\vec{F}\cdot\vec{dr}=E_k(\vec{r_b})-E_k(\vec{r_a})=E_p(\vec{r_a})-E_p(\vec{r_b})\)
质点在一个保守力租用下,使得它在某个空间区域内的每一个点位置具有由该位置确定的能量。这个能量称为位能或者势能\(E_p(\vec{r})\)
质点从一个位置到另一个位置,它的势能减少量等于位移过程中该保守力的做功量
\(-dE_p=\vec{F}\cdot\vec{dr}\)
如果设定某一个\(r_0\)点位置,让它的\(E_p(\vec{r_0})=0\),\(\vec{r_0}\) 称为势能零点,则给定某一点的势能就可以确定。
重力势能
势能零点:任意选取
\(E_p(h)=mgh\)
胡克弹性力的势能
势能零点:选x=0处
\(E_p(x)=\frac{1}{2}kx^2\)
惯性离心势能
\(\vec{F_c}=m\omega^2\vec{r}\)
势能零点:选\(\vec{r}=0\)处
\(E_p(\vec{r})=-\frac{1}{2}m\omega^2r^2\)
万有引力势能
假设M不动,m可动
\(\vec{F}(\vec{r}\to \infty)=0\),因此取无穷远处为势能零点
\(E_p(\vec{r})=\frac{-GMm}{r}\)
一对保守力的势能
一对真实力势能归两者共有

\(dE_p(\vec{r})=\vec{F_A}\cdot\vec{dr_A}+\vec{F_B}\cdot\vec{dr_B}=\vec{F_B}\cdot\vec{dr}\) 这个之前已经推导过了。
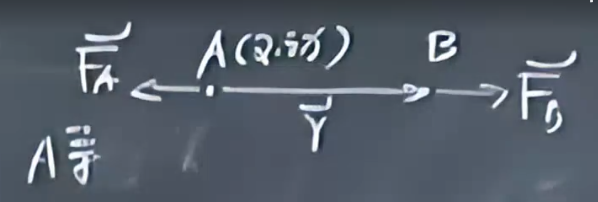
这时转化为一个保守力\(\vec{F_B}\)对应的势能,可以把这个看成一对保守力对应的势能
因此S,A系中\(dE_p(\vec{r})\)相同
例子:一对万有引力的势能
S系中有M,m两个可动的,M系固定M不可动,则S、M系中的\(dE_p(\vec{r})\)一样,都是\(\frac{-GMm}{r}\)
机械能定理
推导
考虑一个质点系,内力分为保守的和非保守的。
考虑第j对保守性内力,对应的势能记为\(E_{p内j}\),引入质点系的内势能\(E_p=\Sigma_j E_{p内j}\)
\(dW_{内保}\):保守性内力做功之和
质点系动能定理:\(-dE_{p内}=dW_{内保}\)
\(dW_{内保}+dW_{内非保}+dW_外=dE_k\)
我们引入\(E=E_k+E_{p内}\)
可以得出质点系机械能定理:\(dW_{内非保}+dW_外=dE\)
机械能守恒
如果恒有\(dW_外=0,dW_{内非保}=0\),则机械能守恒
碰撞
一维碰撞
定义:碰撞前后速度都在同一直线上。
二体碰撞
动量守恒:\(m_1v_1+m_2v_2=m_1v_1'+m_2v_2'\)(带‘的是初速度)
弹性碰撞
解1:\(v_1=v_1'\), \(v_2=v_2'\)
解2:\(v_1=\frac{(m_1-m_2)v_1'+2m_2v_2'}{m_1+m_2}\)
\(v_2=\frac{(m_2-m_1)v_1'+2m_1v_2'}{m_1+m_2}\)
\(v_2-v_1=v_1'-v_2'\)(速度差保持不变)
观察:原因具有1,2置换对称性,结果也有对称性
\(m_1=m_2\) 则互换速度
完全非弹性碰撞
碰撞后一起运动
\(v_1=v_2=\frac{m1v_1'+m2v_2'}{m_1+m_2}\)
$v_2-v_1=0(v_1'-v_2') $
非弹性碰撞
\(v_2-v_1=e(v_1'-v_2')\) e介于0,1之间,称为恢复系数。
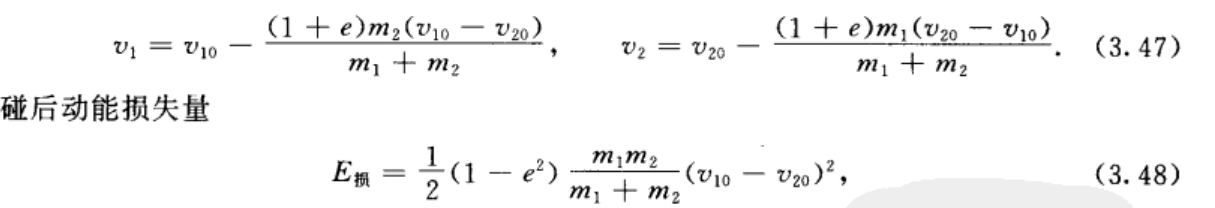
三体碰撞
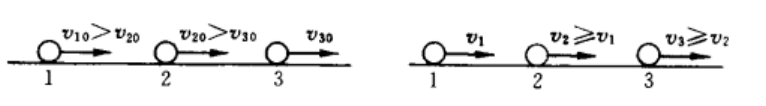
动量守恒:\(m_1v_1+m_2v_2+m_3v_3=m_1v_1'+m_2v_2'+m_3v_3'\)(带‘的初始状态)
完全非弹性碰撞
三个末速度相等,于是有唯一解
弹性碰撞
\(\frac{1}{2}m_1v_1^2+\frac{1}{2}m_2v_2^2+\frac{1}{2}m_3v_3^2=\frac{1}{2}m_1v_1'^2+\frac{1}{2}m_2v_2'^2+\frac{1}{2}m_3v_3'^2\)
解不可以唯一确定,为什么?
这是因为把小球刚性化了,碰撞时具体的挤压被忽略了,与真实的情况不同了。丢了几何结构和物质结构。后续讨论的斜碰撞考虑了几何结构。
绳子类碰撞作用
\(m_1\),\(m_2\)两个小球由软绳连结。2初速度\(v_2'\)大于1初速度\(v_1'\),求绳子伸直后的运动状态。
动量守恒:\(m_1v_1+m_2v_2=m_1v_1'+m_2v_2'\)
情况1:假设绳子不损耗机械能,则可以看成类弹性碰撞
情况2:绳子一旦伸直不再回缩
\(v_1=v_2\),类完全非弹性碰撞
情况3:介于情况1,情况2之间
\(v_1-v_2=e(v_2'-v_1')\),类非弹性碰撞
二维斜碰撞
定义:碰撞前后速度矢量在同一平面内
二体碰撞
动量守恒:\(m_1v_1+m_2v_2=m_1v_1'+m_2v_2'\)(带‘的是初速度)
完全非弹性碰撞
\(v_1=v_2=\frac{m_1v_1'+m_2v_2'}{m_1+m_2}\)
解确定
弹性碰撞
\(\frac{1}{2}m_1v_1^2+\frac{1}{2}m_2v_2^2=\frac{1}{2}m_1v_1'^2+\frac{1}{2}m_2v_2'^2\)
解不确定
解决这种不确定性,可以补充一个标量方程,也可以给出一些碰撞过程的相互作用细节,或者给出几何结构。在我们讨论宏观问题时,突破口往往是几何结构。
例子:在一个光滑水平面上有两个相同的小球1号2号,1号一开始静止,2号一开始有如图所示的初速度。求碰后的状态。

我们可以把2初速度分为\(v_\perp\)和\(v_\parallel\)
题目
题1
很小的定滑轮与轻绳之间无摩擦,绳的A端由变力F拉动,使A始终具有水平速度\(v_0\),系统的其他参量均已在图中给存储,求F的功率P
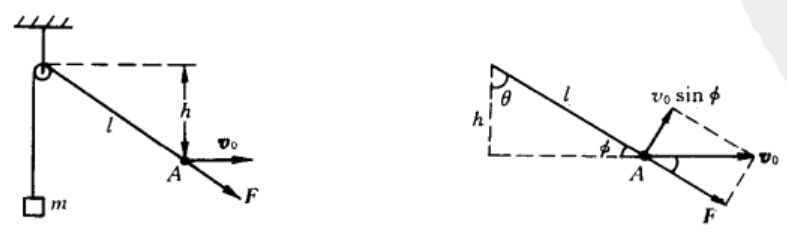
\(P=\vec{F}\cdot\vec{v}\)
F=T
\(T-mg=ma_m\)
回顾:平面极坐标系中的内容
极坐标系中径向加速度:\(a_r=\frac{d^2r}{dt^2}-r(\frac{d\theta}{dt})^2\)
在这里我们把滑轮看作极坐标系的原点,因为\(a_r=0\),所以我们可以得出\(a_m=\frac{d^2r}{dt^2}=\frac{v_0^2h^2}{l^3}\)
最终可以解出\(P=m(g+\frac{v_0^2h^2}{l^3})v_0\frac{\sqrt{l^2-h^2}}{l}\)
题2
一个均匀的柱形弹性体,整体质量M,劲度系数k,自由长度L。用手托着到原来的长度,求手的托力\(F_0\)是多少?
手逐渐往下移动,计算一下手从初始位置到手刚好离开柱体,做的\(W_F\)是多少?
解答:
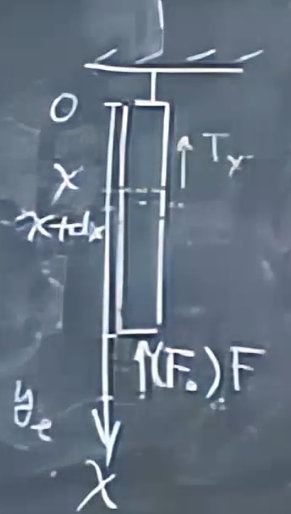
从上到下建立x坐标轴,最上面为零点
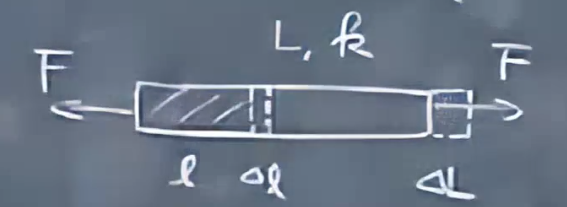
考虑这个柱体横着放置,取它长度为l的一段。给柱体左右都施加力F。
\(\frac{\Delta l}{\Delta L}=\frac{l}{L}\)
\(F=k\Delta L\) ; \(F=k_l \Delta l\)
\(k_l=\frac{\Delta L}{\Delta l}k=\frac{L}{l}k\)
\(k_{dx}=\frac{L}{dx}k\)
手的托力F,\(T_x=\frac{L-x}{L}Mg-F\)
dx的伸长量:\(d\phi=\frac{T_x}{k_{dx}}=(\frac{L-x}{L}Mg-F)\frac{dx}{kL}\)
\(y=\int_{0}^{L}d\phi=\frac{Mg}{2k}-\frac{F}{k}\)
\(F_0对应y=0,为\frac{1}{2}Mg\)
\(W=\int_{0}^{y_1}-Fdy\)(手向下移动,dy向下,但是F向上,所以负号)
\(F=\frac{1}{2}Mg-ky\)
F=0对应\(y_1=\frac{Mg}{2k}\)
\(W=-\frac{1}{8}\frac{M^2g^2}{k}\)
这里有一个值得注意的结论,长度为\(\frac{1}{n}\)原长,劲度系数变为n倍
题3
本题考查参考系的选取

(1)求AB间距最大值\(l_{max}\)
(2)求从开始时刻到AB间距最大的时候,\(W_F\)
解答:
想办法把\(W_F\)甩掉,取B参考系。没有外力和非保守力做功,因此机械能守恒。
末态\(0-\frac{GMm}{l_{max}}=\frac{1}{2}mv_0^2-\frac{GMm}{l_0}\)初态
\(l_{max}=\frac{2l_0GM}{2GM-l_0v_0^2}\)
正常参考系:
\(末态:\frac{1}{2}(m+M)v_0^2-\frac{GMm}{l_m}\)
\(初态:\frac{1}{2}Mv_0^2-G\frac{Mm}{l_0}\)
\(W_F=末-初\)
解出\(W_F=mv_0^2\)
讨论到这里是不完备的,第一问的答案是否有意义取决于\(v_0\)
补充讨论:

题4
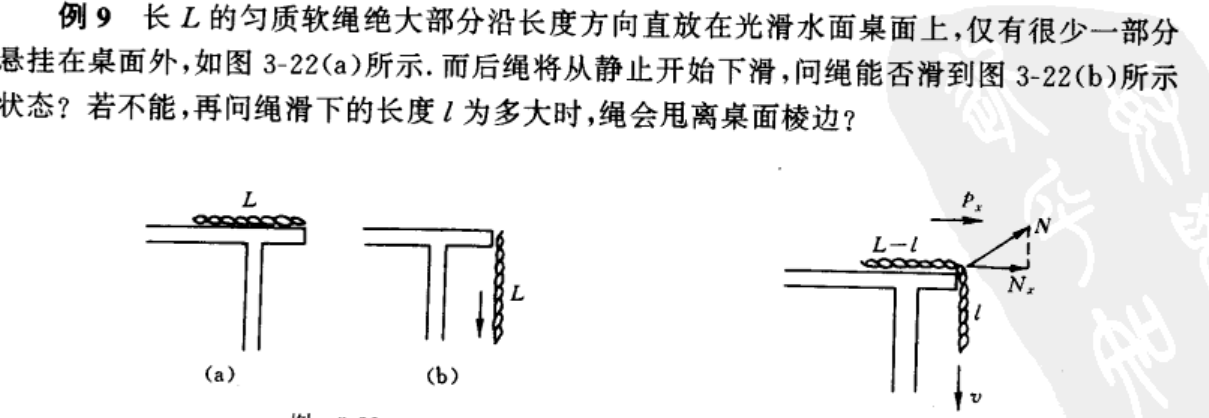
一开始\(P_x=0\),当绳子开始下滑的时候,\(P_x\)显然大于0。如果最终能达到中间的图所示的那种状态,必然有一个\(P_x\)减小的过程。
唯一能够改变\(P_x\)的外力是桌角给的支持力\(\vec{N}\),显然这个力只能斜向上,所以\(P_x\)不可能减小。
当N=0时,意味着要分离了,此时有\(P_x\)最大值。
设\(\lambda\)为绳子的线密度,将绳子的运动速率记为v,则有能量关联式:
\(\frac{1}{2}(\lambda L)v^2=(\lambda l)g\frac{l}{2}\)
\(得出v=\sqrt{\frac{g}{L}}l\)
因此\(p_x=\lambda (L-l)v=\lambda (L-l)\sqrt{\frac{g}{L}}l\)
显然\(l=\frac{1}{2}L\)时水平动量最大,离开桌面。
题5

这个转换方式很巧妙,对于直角三角形的关系,要多注意斜边中点的特性。

题6
A球初始位置\(H_A\),B球初始位置\(H_B\),二者质量相同。所有的碰撞都是弹性的,求AB构成的系统周期运动的条件是什么?
解答:
本题的特殊性在于AB质量相同,质量相同的物体弹性碰撞会交换速度。于是我们讨论A,B两类运动状态。
A类运动状态的承担者:A,B,A,B....
B类运动状态承担者:B,A,B,A....
\(T_A=2\sqrt{\frac{2H_A}{g}}\)
\(T_B=2\sqrt{\frac{2H_B}{g}}\)
两类运动状态构成的系统是不是有公共的周期?
条件:\(T_A,T_B\) 有最小公倍数,即\(\frac{T_A}{T_B}\) 为有理数(\(\frac{N_A}{N_B}\))。
即高度之比为一个有理数的平方。
如果不发生三体碰撞呢?
要求\(N_A\)和\(N_B\)一奇一偶
题7
一个光滑椭圆环固定在一个光滑水平面上,椭圆的周长为L,一个小球贴着椭圆环的内侧匀速率v运动。旋转一个周期,在这一个周期内,计算弹力F大小的平均值是多少(对时间求平均)?
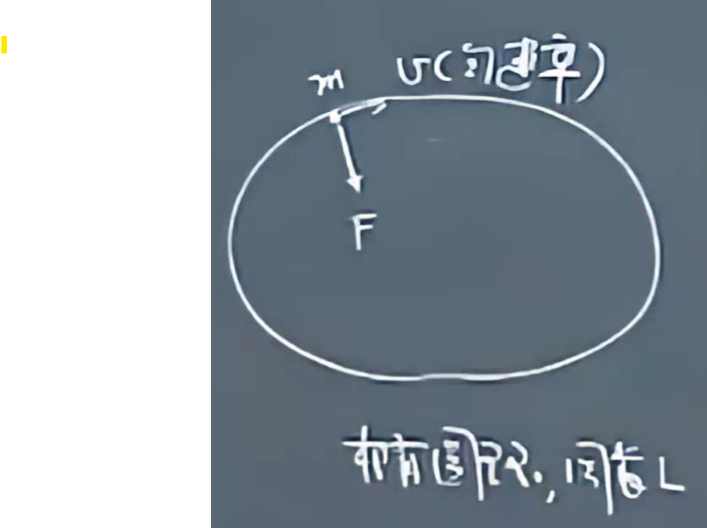
解答:
\(F=\frac{mv^2}{\rho}\)
\(F_平=\frac{\int_T Fdt}{T}\)
\(Fdt=mv(\frac{vdt}{\rho})=mv\frac{dl}{\rho}=mvd\theta\)
\(F_平=\frac{\int_{0}^{2\pi} mvd\theta}{T}\)
\(F_平=\frac{2\pi mv^2}{L}\)
题8
考查斜碰撞中摩擦力起的作用
小球从h自由下落,落在向右以\(v_0\)运动的平板上,把竖直方向与平板的碰撞是弹性碰撞。小球和平板摩擦系数为\(\mu\),求弹回去的速度。
解答:
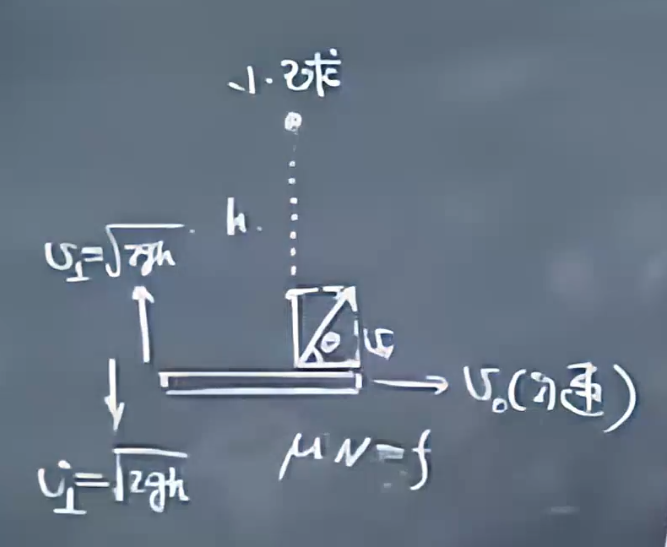
\(N\Delta t =2m v_\perp\)
\(f\Delta t=m v_\parallel\)
\(f=\mu N\)
\(v\perp=\sqrt{2gh}\)
可以解出\(v_\parallel\)
注意:如果\(v_\parallel>v_0\),则上述结论失效,取\(v_\parallel=v_0\)
题9
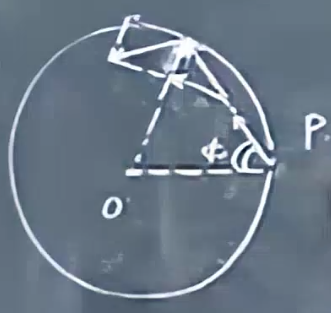
光滑的水平面上有一个质量均匀分布的光滑圆环(不固定),圆环的右侧开一个小孔(引起的质量损失忽略不计)。有一个小球P从小口进入圆环,速度与径向夹角为\(\phi\)。问\(\phi\)取何值的时候,小球可以在圆里面兜圈子,最后还从小孔出去?
解答:
碰撞的时候,切向速度保留。
这道题目并没有给出质量,我们可以利用相对速度大小来求解。因为相对速度大小不变,碰撞后相对于圆环的运动与固定圆环不动时碰撞后的运动相同(类似于光的反射)
因此,\(\phi\) 需要为正多边形对应的角度,包括\(\phi=0\)