角动量定理与天体运动

角动量定理

质点角动量定理

概念引入

质点速度\(\vec{v}\)：是一个相对参考系整体的运动学量

不同的参考系可以测量出不同的\(\vec{v}\)，在同一参考系内相对不同参考点（参考点相对参考系不动）具有相同的\(\vec{v}\)

动量、动能也有相似性质

刻画质点相对同一参考系，不同参考点有不同效果的是质点相对这个参考点的旋转运动。为了描述这种效果，我们引入面积速度。

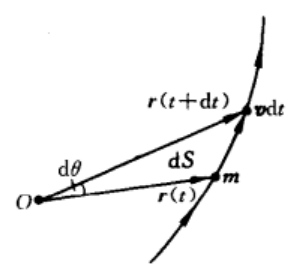
\(dS=\frac{1}{2}|\vec{r}\times\vec{v}dt|\)

引入面积速度\(k=\frac{dS}{dt}=\frac{1}{2}|\vec{r}\times\vec{v}|\)

矢量化为\(\vec{k}=\frac{1}{2}\vec{r}\times\vec{v}\)

速度\(\vec{v}\)对应动量\(\vec{P}\)

类似地，面积速度\(\vec{k}\)对应角动量\(\vec{L}=2m\vec{k}=\vec{r}\times\vec{P}\)

\(\vec{k}和\vec{L}\)相对不同参考系和同意参考系的不同参考点是不同的。

为什么速度\(\vec{v}\)随着t变化？我们有\(\frac{\vec{dP}}{dt}=\vec{F}\)

类似地，面积速度\(\vec{k}\)是否随着t变化？我们通过\(\frac{dL}{dt}\)确定。

\(\frac{dL}{dt}=\frac{d(\vec{r}\times\vec{p})}{dt}=\frac{d\vec{}r}{dt}\times\vec{P}+\vec{r}\times\frac{d\vec{P}}{dt}=\vec{r}\times\vec{F}\)

这是因为\(\frac{\vec{dr}}{dt}=\vec{v}\)和\(\vec{P}\)平行，叉乘为零。

于是我们引入力矩\(\vec{M}=\frac{d\vec{L}}{dt}=\vec{r}\times\vec{F}\)

角动量守恒

若过程中恒有\(\vec{M}=0\),则\(\vec{L}\) 整体守恒

若某个分量力矩恒为零，则角动量在这个分量上守恒

例子

匀速圆周运动

质点做匀速圆周运动，相对O角动量守恒。因为向心力指向圆心，力矩为零。

行星运动

找太阳所在位置F，相对F角动量守恒。

圆锥摆

竖直方向上角动量守恒

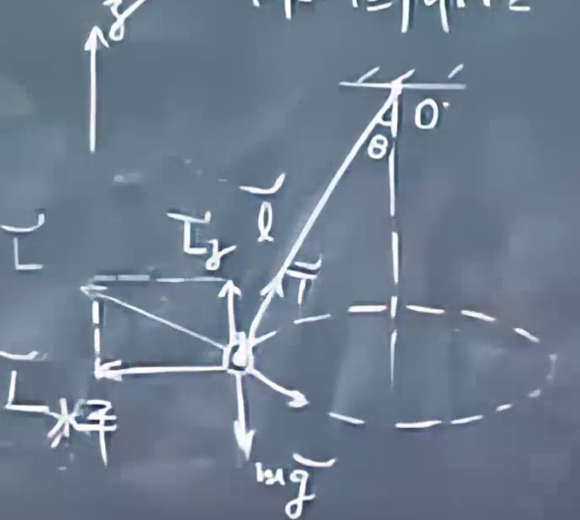
摆线长度l，半顶角\(\theta\)。取悬挂点O为参考点。

分析方式1：用力矩

\(\vec{M}=\vec{l}\times mg\)

\(\vec{M}\)水平旋转，方向指向纸面外，\(\vec{M_z}=0\)（竖直方向上角动量守恒）

分析方式2：直接分析

\(\vec{L}=\vec{l}\times m\vec{v}\) 斜向上，旋转

\(\vec{L_水}\)旋转，\(\vec{L_z}\)守恒量

单摆

取指向纸面外为z轴

\(\vec{M}=\vec{l}\times(\vec{T}+m\vec{g})=\vec{l}\times m\vec{g}\)

\(\vec{M}=-lmgsin\theta \vec{k}\), \(\vec{k}\)是z轴正方向的方向向量

\(\vec{L}=\vec{l}\times m\vec{v}=lmv\vec{k}\)

\(v=l\frac{d\theta}{dt}\)

\(\vec{L}=ml^2\frac{d\theta}{dt}\vec{k}\)

由质点角动量定理，\(\vec{M}=\frac{d\vec{L}}{dt}\)

\(-lmgsin\theta=ml^2\frac{d^2\theta}{dt^2}\)

\(\frac{d^2\theta}{dt^2}+\frac{g}{l}sin\theta=0\)

若取小角度，可近似把\(sin\theta=\theta\)

即\(\frac{d^2\theta}{dt^2}+\frac{g}{l}\theta=0\)

注意到这个方程与简谐运动方程数值上同构

简谐运动方程：\(\frac{d^2x}{dt^2}+\omega^2\theta=0\)

质点系角动量定理

惯性系

引理：

一对作用力与反作用力相对同一参考点力矩和为0

S系由1，2两个质点构成，参考点为O，1的位置是\(\vec{r_1}\),2的位置是\(\vec{r_2}\) 表示从1指向2的矢量为\(\vec{r}\)

\(\vec{r_1}\times\vec{F_1}+\vec{r_2}\times\vec{F_2}=(-\vec{r_1}+\vec{r_2})\times\vec{F_2}=\vec{r}\times\vec{F_2}\)

因为\(\vec{r}\)和作用力同一方向，因此力矩之和为零。

定义：\(\vec{L}=\Sigma_i\vec{L_i}\)

\(\frac{\vec{dL}}{dt}=\Sigma_i\frac{d\vec{L_i}}{dt}=\Sigma\vec{M_i}\)

因为作用力与反作用力之和为零，故内力力矩为零。我们可以得出：

质点系角动量定理：\(\vec{M_外}=\frac{d\vec{L}}{dt}\)，\(M_外\)是外力力矩之和。

非惯性系

\(\vec{F'}=\vec{F_真}+\vec{F_惯}=m\vec{a'}\)

\(\vec{M_外}+\vec{M_惯}=\frac{d\vec{L}}{dt}\)，\(M_惯\)是惯性力矩之和

角动量守恒定律

如果恒有\(\vec{M_外}=0\) 则质点系角动量守恒

天体运动

二体引力系统

把其中一个天体看作不动，简化为一体运动

开普勒三定律

轨道定律

可以引申为圆锥曲线运动轨道。椭圆、抛物线、双曲线。焦点是太阳的位置。

轨道能量\(E_p\)。椭圆\(E_p<0\),抛物线\(E_p=0\),双曲线\(E_p>0\)

到ep2，先鸽了，学质心刚体去了

题目

题1

圆锥面光滑，小球一开始在高度为H做匀速圆周运动，给小球一个冲量，使其速度变成\(\sqrt{1+\alpha}\)倍。求小球上升的最大高度

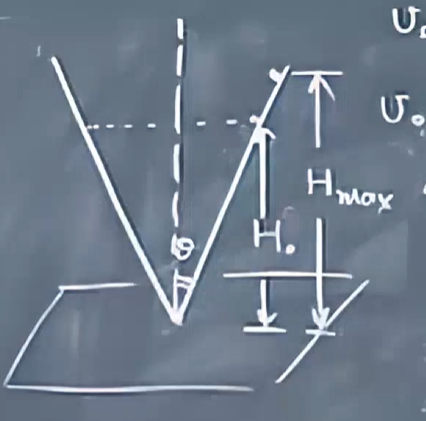
可以通过牛顿定律算出小球做圆周运动的速度是\(v_0=\sqrt{gH_0}\)

突破口：取O点为参考点，发现\(M_z=0\)，即\(L_z\)守恒（z方向是竖直方向）

这个角动量守恒关系结合能量守恒就可以求解