质心与刚体

质点系与刚体

刚性质点系

性质与定义（chap1）

定义：每两个质点的间距不变。刚体是一种特殊的刚性质点系。

自由度：

取出三个不共线的质点，那么可以唯一确定一个平面。命名为1，2，3号质点。如果\(\vec{r_1},\vec{r_2},\vec{r_3}\)确定，可以确定整个系统所有点的位置。此时自由度取决于1，2，3.

1，2，3还有三个约束方程（来刻画距离不变）

因此刚性质点系运动的参量只有6个。

内力：内力冲量、做功不变，内力力矩之和为零

运动的分解

随基点的平动——自由度为3（xyz）

绕基点的转动——自由度为3（进动、自转、章动）

质心（c）

为刚性质点系寻找一个点部位，它的运动与内力无关，因此我们引入质心。

位置：

（惯性）质量分布中心：\(\vec{r_c}=\frac{\Sigma_i m_i\vec{r_i}}{\Sigma_i m_i}\)

质量：

\(m_c=\Sigma_i m_i\)

或者我们可以这么刻画质心：

\(\vec{r_c}=\frac{\Sigma m_i\vec{r_i}}{m_c}\)

\(x_c=\frac{\Sigma m_ix_i}{m_c}\)

\(y_c=\frac{\Sigma m_iy_i}{m_c}\)

\(z_c=\frac{\Sigma m_iz_i}{m_c}\)

质心引申为质点系共有的力学概念。

质心的位置

二质点系

\(x_c=\frac{m_1x_1+m_2x_2}{m_1+m_2}\)

令\(x_c=0\)

则\(m_1x_1+m_2x_2=0\)

令\(|x_1|=l_1\) \(|x_2|=l_2\)

\(l_1+l_2=l（二者间距）\)

则\(l_1=\frac{m_1}{m_1+m_2}l\)

\(l_2=\frac{m_2}{m_1+m_2}l\)

三质点系

可以把1，2先找到一个质心，把这个问题转化为二质点系问题。

质心组合关系

将质点系分成若干小系，各小系质心构成的质点系，其质心即为原质点关系的质心

匀质细杆

左右取对称的，因此质心在中点。

匀质三角板

从上到下切成若干细杆，再从左到右切成若干细杆。质心在两条中线之交点，即重心。

匀质三角形框架

三条边质心均在中点位置，但注意质量与边长成正比。

结合角平分线定理，可以知道整个质心在内心上。

质心运动定理

\(m_c\vec{r_c}=\Sigma m_i\vec{r_i}\)

两边对t求导

\(m_c\vec{v_c}=\Sigma m_i\vec{v_i}\)

由质点系动量定理，\(\vec{F_{合外}}=\frac{\vec{dP_c}}{dt}=m_ca_c\)，这就是惯性系中的质心运动定理

惯性系中的质心动能定理\(W_{\vec{F_{合外}}}=\Delta E_{kc}\)

质点系动力学量的分解

以下结论对惯性系和非惯性系均成立

\(\vec{P}=\vec{P_c}\) 或者 \(\vec{P}=\vec{P_c}+\vec{P'}(\vec{P'}=0)\)

\(E_k=E_{kc}+E_k'\) , \(E_k'\)代表质点系相对质心的动能

\(\vec{L}=\vec{L_c}+\vec{L'}\) , \(\vec{L'}\)代表质点系相对质心的角动量

若干质点发生多体碰撞：

\(\vec{P},\vec{P_c},\vec{v_c}\)不变，因此\(E_{kc}\)不变，损失的动能来自\(E_k'\)。完全非弹性碰撞时，\(E_k'\)完全损失为零。

质心参考系

定义：随质心一起（相对惯性系）运动的参考系。这是一个平动参考系。

若\(\vec{F_{合外}}=0\) 则 \(\vec{a_c}=0\) 质心系为惯性系

若\(\vec{F_{合外}}\not =0\) 则 \(\vec{a_c}\not=0\) 质心系为非惯性系，此时会出现平移惯性力。

为了方便，质心系中一致地引入平移惯性力\(\vec{F_i}=m_j(-\vec{a_c})\)将\(\vec{a_c}=0\)处理为特例

质心系中的质点动力学定理

动量定理

\(\vec{P}=0\) 因为质点系动量等于质心动量

动能定理

\(dW_惯+dW_内+dW_外=dE_k\)

\(dW_惯=\Sigma ma_i(-\vec{a_i})\cdot \vec{dr_i}\)

\(dW_惯=-\Sigma m_i\vec{dr_i}\cdot \vec{a_c}=-\Sigma d(m_i\vec{r_i})\cdot \vec{a_c}\)

\(dW_惯=-d(m_c\vec{r_c})\cdot \vec{a_c}\)

\(r_c\)是质心在质心系的位矢，因此\(d\vec{r_c}=0\)

于是动能定理可以被简化为：\(dW_内+dW_外=dE_k\)

或者：\(W_内+W_外=\Delta E_k\)

角动量定理

\(\vec{M_惯}+\vec{M_外}=\frac{d\vec{L}}{dt}\)

\(\vec{M_惯}=\Sigma \vec{r_i}\times m_i (-\vec{a_c})=-\Sigma m_i\vec{r_i}\times \vec{a_c}\)

\(\vec{M_惯}=-m_c\vec{r_c}\times \vec{a_c}\) 一般情况下不为零，但如果取质心为参考点，则这一项为零。

取质心为参考点：\(\vec{M_外}=\frac{d\vec{L}}{dt}\)

刚体定轴转动

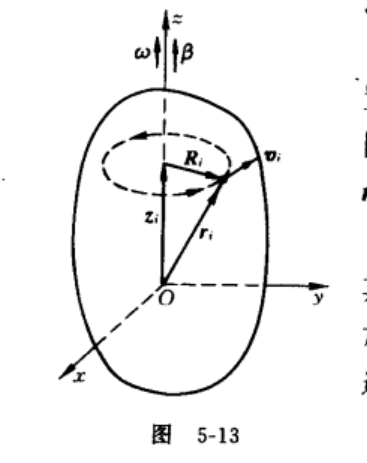
运动学描述

\(\omega\) \(\beta\)

\(\vec{r_i}=\vec{z_i}+\vec{R_i}\) 分解

\(\vec{v_i}=\omega R_i\)

\(a_{i心}=\omega^2 R_i\)

\(a_{i切}=\beta R_i\)

动力学描述

\(E_k=\Sigma \frac{1}{2}m_iv_i^2=\frac{1}{2}\Sigma m_i R_i^2 \omega^2\)

记$I=m_i R_i^2 $ 则 \(E_k=\frac{1}{2}I\omega^2\)

我们将I称为转动惯量

刚体的内势能是一个不变量

角动量（O为参考点）

\(\vec{L}=\Sigma \vec{r_i}\times(m_i\vec{v_i})=\Sigma \vec{z_i}\times(m_i\vec{v_i})+\Sigma \vec{R_i}\times(m_i\vec{v_i})\)

拆出来的第一项是\(\vec{L}\)在xy平面上分量

拆出来的第二项是\(\vec{L}\)在z轴方向分量

考虑\(\vec{L_z}=\Sigma m_iR_iv_i= \Sigma m_iR_i^2 \omega\)

因此\(\vec{L_z}=I\omega\)

转动惯量

匀质细杆

质量为M，长度为L

绕中点转

建立坐标轴，取中点为O点。

用微元法，取一小段\(m_i\) 则\(dm=\frac{dx}{L}M\)

\(R_i=x\)

\(\Sigma m_i R_i^2=\int_{-\frac{1}{2}L}^{\frac{1}{2}L}dm x^2\)

\(I=\frac{1}{12}ML^2\)

绕端点转

\(\int _{0}^{L}\frac{dx}{L}Mx^2=\frac{1}{3}ML^2\)

匀质长方版

长L质量M

绕中央轴转

\(I=\frac{1}{12}ML^2\)

绕左边或右边转

\(I=\frac{1}{3}ML^2\)

圆环/圆筒绕圆心

\(I=MR^2\)

因为每一个点与圆心距离都是R

匀质圆盘/圆柱绕圆心

看成很多个圆环的累加

取半径为r的一小个小圆环dr

\(dI=\frac{2\pi r dr}{\pi R^2}r^2\)

\(I=\frac{1}{2}MR^2\)

平行轴定理

已知刚体质量为M，绕过质心C的轴转动惯量为\(I_c\)，PQ轴与该轴平行，与该轴距离为d。绕PQ转动的\(I_{pq}与I_c\)关系是什么？

假设绕PQ转动角速度为\(\omega\)

\(E_k=\frac{I_{PQ}}{\omega^2}\)

根据质点系动能：\(E_k=E_{kc}+E_k'\)质心动能加上质点系相对质心动能

\(E_k=\frac{1}{2}Mv_c^2+\frac{1}{2}I_c\omega^2\)(相对C旋转角度和想到对PQ旋转角度一样)

\(v_c=\omega d\)代入

得\(I_{PQ}=I_c+Md^2\)

匀质正方版绕对角线

运用平行轴定理做递推，设\(I=\alpha ML^2\)

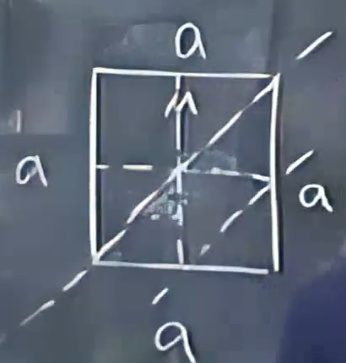
把左上右下的小正方形在平移到原转轴上，写出递推关系式解出\(\alpha\)

垂直轴定理

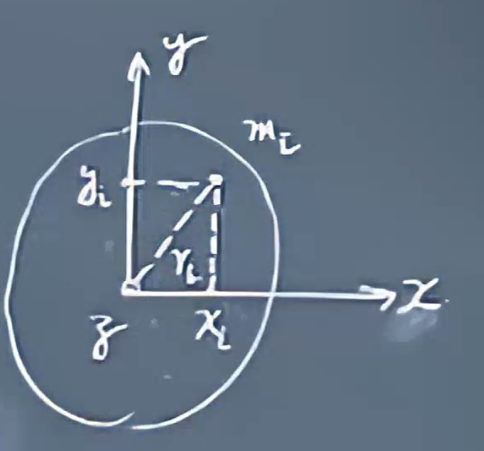
\(I_x=\Sigma m_iy_i^2\)

\(I_y=\Sigma m_ix_i^2\)

\(I_x+I_y=\Sigma m_i(y_i^2+x_i^2)=\Sigma m_ir_i^2=I_z\)

\(I_z=I_x+I_y\)

匀质正方形薄版

绕着斜轴MN旋转

取\(PQ\perp MN\)

由于对称性，显然\(I_{MN}=I_{PQ}\),\(I_x=I_y\)

\(I_{MN}=\frac{1}{2}I_z=I_x\)

因此\(I_{MN}=\frac{1}{12}Ma^2\)

匀质球壳

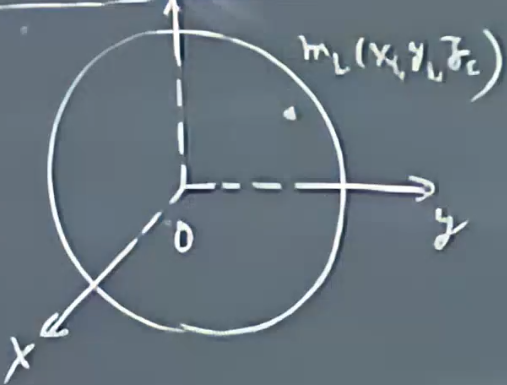
绕x轴旋转转动惯量\(I_x=\Sigma m_i(y_i^2+z_i^2)\)

绕y轴旋转转动惯量\(I_y=\Sigma m_i(x_i^2+z_i^2)\)

绕z轴旋转转动惯量\(I_z=\Sigma m_i(y_i^2+x_i^2)\)

于是\(I_x+I_y+I_z=2\Sigma m_i R^2=2MR^2\)

\(I_x=I_y=I_z=I_{直径}\)

因此\(I_{直径}=\frac{2}{3}MR^2\)

动力学定理

质心运动定理

质心运动定理：\(\vec{F_{合外}}=m\vec{a_c}\)

动能定理：\(dW_外=dE_k\)，\(E_k=\frac{1}{2}I\omega^2\)

转动定理（角动量定理沿着转轴方向的分量式）\(M_{外z}=\frac{dL_z}{dt}=I\beta\)

刚体平面平行运动

定义：每一个点部位都在自己对应的一个平面内运动，所有这些平面彼此平行

运动学内容

对刚体进行投影到\(\sigma\)平面上

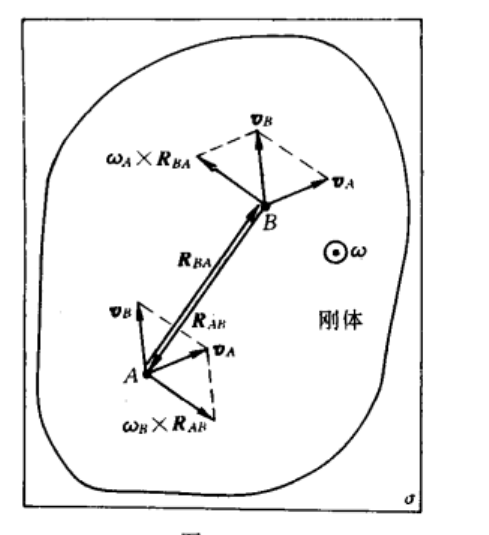
角速度相对任意一个分解点都一样

运动分解为：随某点部位的平动&绕该点部位的转动

“某点”取A，则B也有相同的\(\vec{v_A}\)。B点绕A点的旋转\(\vec{\omega_A}\)。则\(\vec{v_B}=\vec{v_A}+\vec{\omega_A}\times R_{BA}\)

“某点”取B，则\(\vec{v_A}=\vec{v_B}-\vec{\omega_B}\times R_{BA}\)

推出\(\vec{\omega_A}\times R_{BA}=\vec{\omega_B}\times R_{BA}\)

因此\(\omega_A=\omega_B=\omega\)

速度瞬心

某时刻速度为零的点称为该时刻的速度瞬心（线）

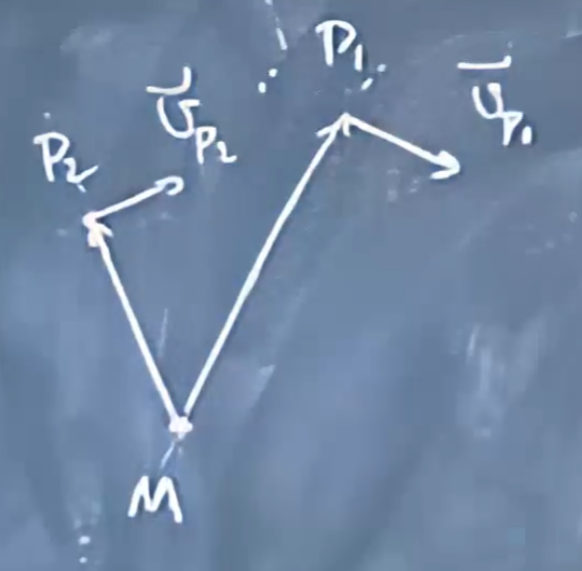
该时刻刚体其他点部位（P）速度等于此点部位相对瞬心（M）运动速度

注意这个关系只有速度相等，其他的运动量不一定相等，因此我们不能说“P相当于绕着M旋转”。譬如\(\vec{a_p}=\vec{a_{PM}}+\vec{a_M}\),可见加速度并不相等。

\(\vec{v_P}=\vec{\omega}\times\vec{R_{PM}}\)

瞬心的寻找

动力学内容

将运动分成随质心平动（外参考系），绕过质心转轴的转动（质心系）

相对外惯性系

质心运动定理：\(\vec{F_{合外}}=m\vec{a_c}\)

动能定理：\(W_外=\Delta E_k\) \(E_k=\frac{1}{2}mv_c^2+\frac{1}{2}I_c\omega^2\)

相对质心系

质心运动定理:\(M_外=I_c\beta\)

动能定理:\(W_外=\Delta E_k\) \(E_k=\frac{1}{2}I_c\omega^2\)

刚体定点转动与平衡

先跳过，大脑过载了。往届讲义似乎没有这部分内容不学了。

习题

题1

一个细杆，\(\lambda_x=\frac{\lambda_0}{L}x\)，求\(x_c\)

\(x_c=\frac{\Sigma m_ix_i}{\Sigma m_i}\)

取一小段，称为i

\(m_i=\lambda_x dx=\frac{\lambda_0}{L}xdx\)

\(x_i=x\)

\(\Sigma m_ix_i=\int_{0}^{L}\frac{\lambda_0}{L}x^2dx=\frac{\lambda_0}{3}L^2\)

\(\Sigma m_i=\frac{1}{2}\lambda_0 L\)

因此\(x_c=\frac{2}{3}L\)

题2

质点A,B质量均为m，A带正电荷q。电场强度E水平向右。AB之间弹性碰撞不交换电荷量。一开始A在B左侧\(l_0\)位置，求从开始到第k次碰撞期间，电场力做的功。

解答：

电场力只对A做功，只需要求出从开始到结束A的位移即可

注意到\(x_A=x_c+\frac{1}{2}l_0\)，\(x_c\)是质心位移

\(a_c=\frac{qE}{2m}\)

计算第一次A向右运动打B所需的时间\(l_0=\frac{1}{2}at_0^2\)

\(t_0=\sqrt{\frac{2ml_0}{qE}}\)

转换参考系，第一次，在B的视角下，A由静止打到B

然后A被反弹，反弹前后相对B的速度相同。这时在B的视角下，A的运动就是第一次的逆过程。

因此\(t_k=(2k-1)t_0\)

\(s_c=\frac{1}{2}a_ct_k^2\) 可以计算

题3

水平地面上等间距地放着10个相同的木块，质量均为m，与地面摩擦系数均为\(\mu\)木块之间均为完全非弹性碰撞。对第一个木块施加恒力F，发现十个木块碰撞到一块的时候正好停下了，求F。

由此可知，合外力对质心做功为零。

质心位移是\(5l_0\)

\(F\cdot 5l_0=\mu mg \frac{1}{9}l_0+2\mu mg \frac{2}{9}l_0+...+9 \mu mg\frac{9}{9}l_0\)

因此我们可以求出F

题4

我们用质心参考系来分析，动能增加为\(2\times \frac{1}{2}mv_{\perp}^2=FL\)

\(v_{\perp}=\sqrt{\frac{FL}{m}}\)

题5

匀质细杆(M，L)由水平静止释放，固定左端点O。求细杆转过\(\theta\)角之后O点所给的支持力的两个分量\(\vec{N_1}\)和\(\vec{N_2}\)

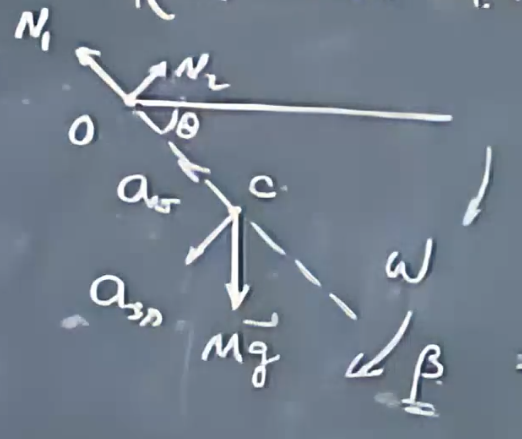
分析:

取O点为参考点，两个力的力矩都为零，因此不能用转动定理。

因为这两个力不做功，不能用动能定理。

因此我们考虑选择质心运动定理来求解。

求解：

我们只需要解出\(\vec{a_心}\)和\(\vec{a_切}\)

\(a_心=\omega^2\cdot \frac{L}{2}\)

通过动能定理可以求出\(\omega\)，重力势能转化为动能

\(a_切=\beta \frac{L}{2}\)

用转动定理，重力所提供的力矩\(M=I\beta\) 可以解出\(\beta\)

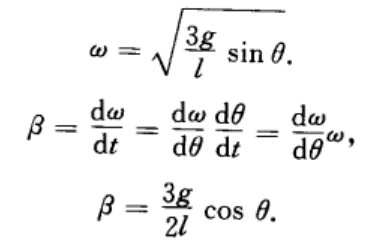
答案：\(N_1=\frac{5}{2}mgsin\theta\) \(N_2=\frac{1}{4}mgcos\theta\)

题6

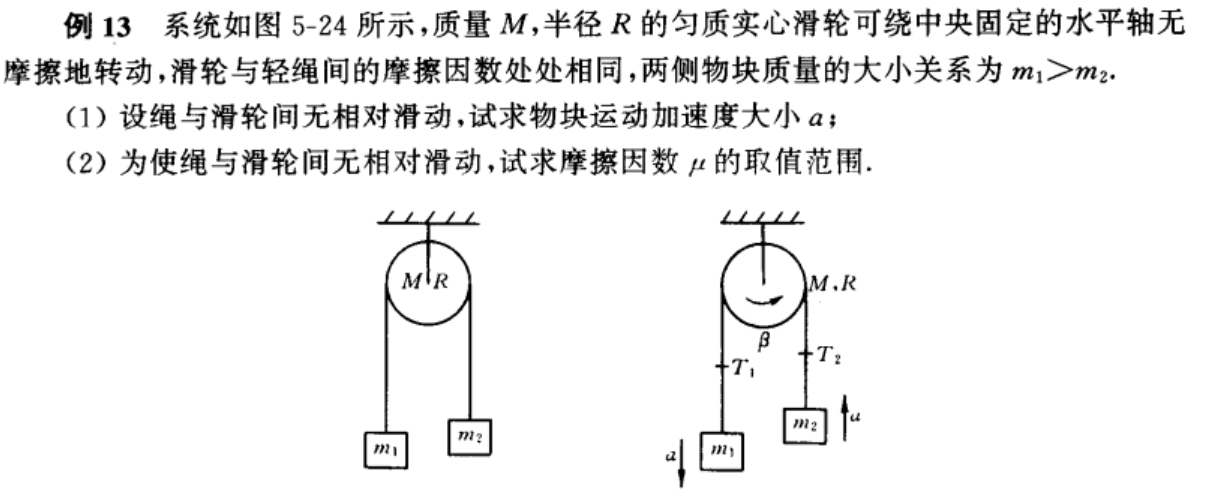
\(m_1g-T_1=m_1a\)

\(T_2-m_2g=m_2a\)

\(T_1R-T_2R=I\beta\) 实际上这个不是原始的方程，原始应该是摩擦力。

注意：高中物理题目往往说“轻质滑轮”，这样能导出一根绳子上拉力相等，但这里滑轮有质量，拉力的力矩不为0，因此两个拉力可以不相等。

运动关联：\(\beta R=a\)

\(a=\frac{2(m_1-m_2)}{M+2(m_1+m_2)}g\)

题7

1. A轴插入前后

以地面A点为参考点，角动量守恒（插入后产生的力相对于A的力矩为零）

\(I_A\omega_A=L_A\) \(\omega_A\)是稳定后的角速度

\(L_A=I_0\omega_0+mv_0\frac{1}{2}L\) 把\(L_A\)分成自转和质心平动两部分,\(v_0=0\)因为O不动

\(I_0\)代表绕着O点旋转的转动惯量\(\frac{1}{12}ml^2\)

解出\(\omega_A=\frac{1}{4}\omega_0\)

2. A轴插入之后

此时\(v_O=\omega_A\frac{L}{2}\)

3. A撤走B插入前后

取地面B为参考点，角动量守恒

\(I_B\omega_B=-mv_O\frac{L}{2}+I_0\omega_A\)

负号是因为质心角动量的r是相对于B算，与\(\omega_A\)相反

\(\omega_B=-\frac{1}{8}\omega_0\)

4. B插入之后

此时\(v_O=\frac{1}{16}\omega_0 L\)

5. B撤走O插入前后

取地面O点位参考点，角动量守恒

\(\omega_BI_0=I_0\omega\)

因此\(\omega=\omega_B=-\frac{1}{8}\omega_0\)

题8 麦克斯韦轮

一边旋转一边向下运动

质心运动:Mg-T=Ma

地面系中不是定轴转动，但在质心系中是定轴（过质心转轴）转动。其动力学方程与惯性系转动定理相同。因为以质心为参考点，惯性力的力矩为零。（详见质心系）

\(TR=I_c\beta\)

\(a=\beta R\)

题9 瞬心加速度

半径为r的圆环A沿着半径为R的固定圆环B的外侧做纯滚动，A的环心O绕着B的环心做圆周运动的角速度记为\(\omega_\theta\),求A环瞬心M的加速度

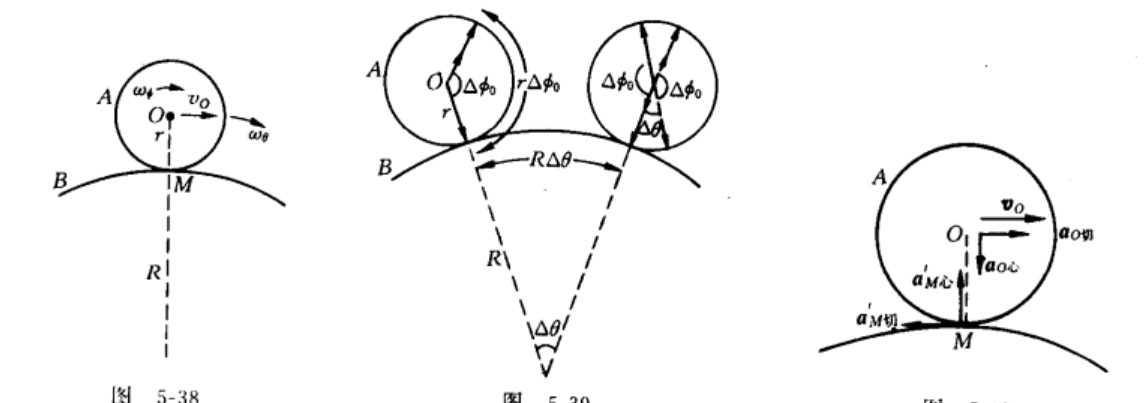
因为A纯滚动，与大圆接触点速度为0，所以M是瞬心

\(v_o=\omega_r\cdot r\)

\(\omega_r=\frac{v_O}{r}\)

\(v_O=(R+r)\omega_\theta\)

\(\omega_\theta=\frac{v_O}{R+r}\)

\(\vec{a_M}=\vec{a_{Mo}}+\vec{a_o}\)

\(\vec{a_{Mo}}\)代表M相对小圆圆心的加速度，因此\(\vec{a_{Mo}}=\omega_r^2r\)方向竖直向上

\(\vec{a_o}=\omega_\theta^2(R+r)\) 方向竖直向下

结果可求出

题10

匀质球体(m,R)放在倾斜角为\(\theta\)的斜面上，我们可以分析出：\(\mu=0\) 纯滑动，\(\mu较小\)，连滚带滑，\(\mu \geq \mu_临\) 进入纯滚动状态，求\(\mu_临\)

加速度：\(mgsin\theta-f=ma\)

角加速度：\(fR=I_c\beta\)

运动关联：\(a=\beta R\)（因为纯滚动\(v=\omega R\)，求导即可）

题11

匀质圆环，m，R。水平地面动摩擦因数\(\mu\)，给圆环水平向右初速度\(v_0\)（初始无旋转），讨论之后圆环的运动

水平向左滑动摩擦力\(f=\mu mg\)

\(v=v_0-at=v_0-\mu gt\)

\(fR=I_c\beta=mR^2\beta\)

\(\omega=\beta t=\frac{\mu g t}{R}\)

当\(v=\omega R\)时，进入纯滚动状态（之后f=0??????????）

题12

匀质细杆质量M，长度L，放在一个光滑水平面上。如图所示有一个小球m，以\(v_0\)打向细杆。球m，M发生第二次碰撞的条件？

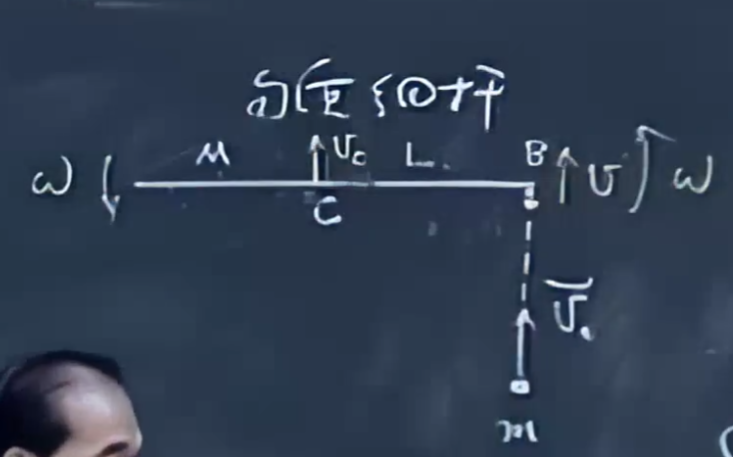
记向上速度方向为正方向

\(\vec{v_c}\)为细杆质心的速度，\(\vec{v}\) 为小球碰撞后的速度

动量守恒:\(Mv_c+mv=mv_0\)

能量守恒:\(\frac{1}{2}Mv_c^2+\frac{1}{2}I_c\omega^2+\frac{1}{2}mv^2=\frac{1}{2}mv_0^2\)

角动量在地面参考系讨论

由细杆和小球组成的系统，相对地面系的任何参考点都守恒。取（移动之前）细杆质心所在点对应地面上的点（记为C点）为参考点。

因此\(0+I_c\omega+\frac{L}{2}mv=\frac{L}{2}mv_0\)（质心平动贡献的角动量是0）

观察可知，发生碰撞的条件是\(v=v_c\)

因此我们可以通过这个关系，找出\(\frac{M}{m}\)的关系，四个未知量四个方程可以求解

题13

光滑水平地面，一个匀质细杆竖直立在水平地面上。给细杆一个扰动让它滑倒。是否有可能细杆整体倒地之前，B端先离开了地面呢？

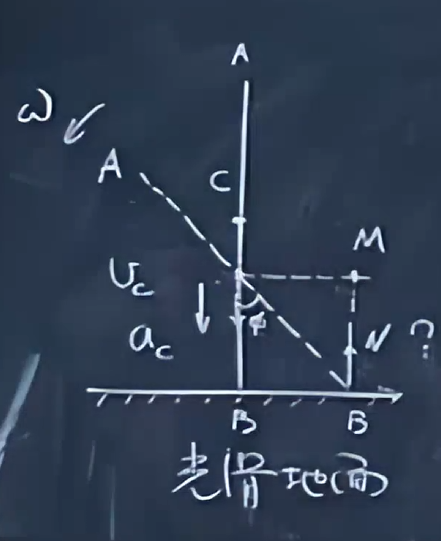
关键点：没有水平外力，因此细杆只有竖直方向的\(a_c\)和\(v_c\)

我们聚焦于N这个量。考虑细杆质心的运动，当\(a_c=g\)的时候，N=0

我们考虑\(a_c与\phi\)的关系

如果\(a_c=\frac{dv_c}{dt}=\frac{dv_c}{d\phi}\frac{d\phi}{dt}\)

我们可以找到瞬心M，\(v_c=\omega\cdot\frac{L}{2} sin\phi\)

用能量守恒，则重力势能减少量=动能增加量

\(Mg\frac{L}{2}(1-cos\phi)=\frac{1}{2}Mv_c^2+\frac{1}{2}I_c\omega^2\)