振动与波
运动学内容
以下讨论简谐振动
运动方程
首先考虑一个匀速圆周运动的直径分运动,把这个分运动称为简谐振动
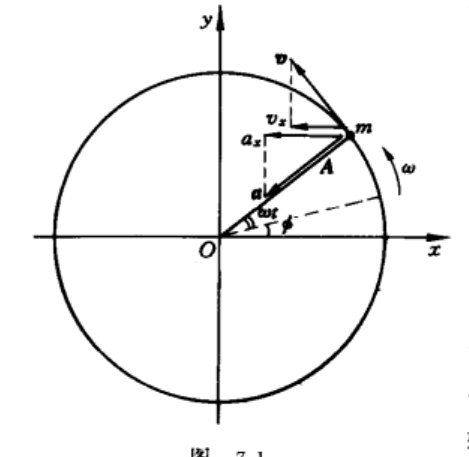
\(x=Rcos(\omega t+\phi)\)
\(v_x=-\omega Rsin(\omega t+\phi)\)
\(a_x=-\omega^2 R cos(\omega t+\phi)\)
注意简谐振动可以写成\(x''+\omega^2 x=0\)的微分方程
将R换成A(振幅取正)
\(\omega\) 角频率
\(\nu=\frac{\omega}{2\phi}\) 频率
\(T=\frac{1}{\nu}=\frac{2\phi}{\omega}\) 周期
\(\omega t+\phi\)称为t时刻振动的相位
\(\phi\) 初相
运动合成
同方向,同频率
\(x_1=A_1cos(\omega t+\phi_1)\)
\(x_2=A_2cos(\omega t+\phi_2)\)
直接相加即可:\(x=x_1+x_2=Acos(\omega t+\phi)\)
\(A=\sqrt{A_1^2+A_2^2+2A_1A_2cos(\phi_2-\phi_1)}\)
\(tan\phi=\frac{A_1sin\phi_1+A_2sin\phi_2}{A_1cos\phi_1+A_2cos\phi_2}\)
若\(\phi_2-\phi_1=2k\pi\) 则\(A=A_1+A_2\) 取得最大值
若\(\phi_2-\phi_1=(2k+1)\pi\) 则\(A=|A_1-A_2|\) 取得最小值
方向振幅初相同,不同频率
\(x_1=Acos(\omega_1t+\phi)\)
\(x_2=Acos(\omega_2t+\phi)\)
\(x=x_1+x_2=2Acos(\frac{\omega_1-\omega_2}{2}t)cos(\frac{\omega_1+\omega_2}{2}t+\phi)\)这不是简谐振动
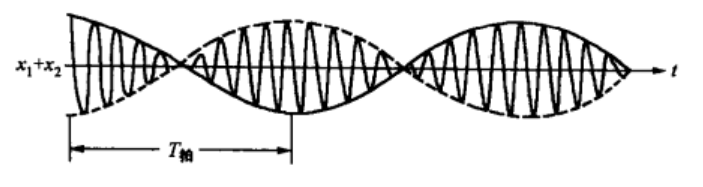
\(cos(\frac{\omega_1-\omega_2}{2}t)\) 可以看成对“振幅”的描述
\(cos(\frac{\omega_1+\omega_2}{2}t+\phi)\)可以看成简谐振动
引入\(\nu_1=\frac{\omega_1}{2\pi}\)和\(\nu_2=\frac{\omega_2}{2\pi}\)
“振幅”绝对值变化的周期频率,也是振幅平方的变化频率,即振动强度的变化频率
\(\nu=2\cdot|\frac{\nu_1-\nu_2}{2}|=|\nu_1-\nu_2|\) 把这个频率称之为拍频率
垂直方向同频率
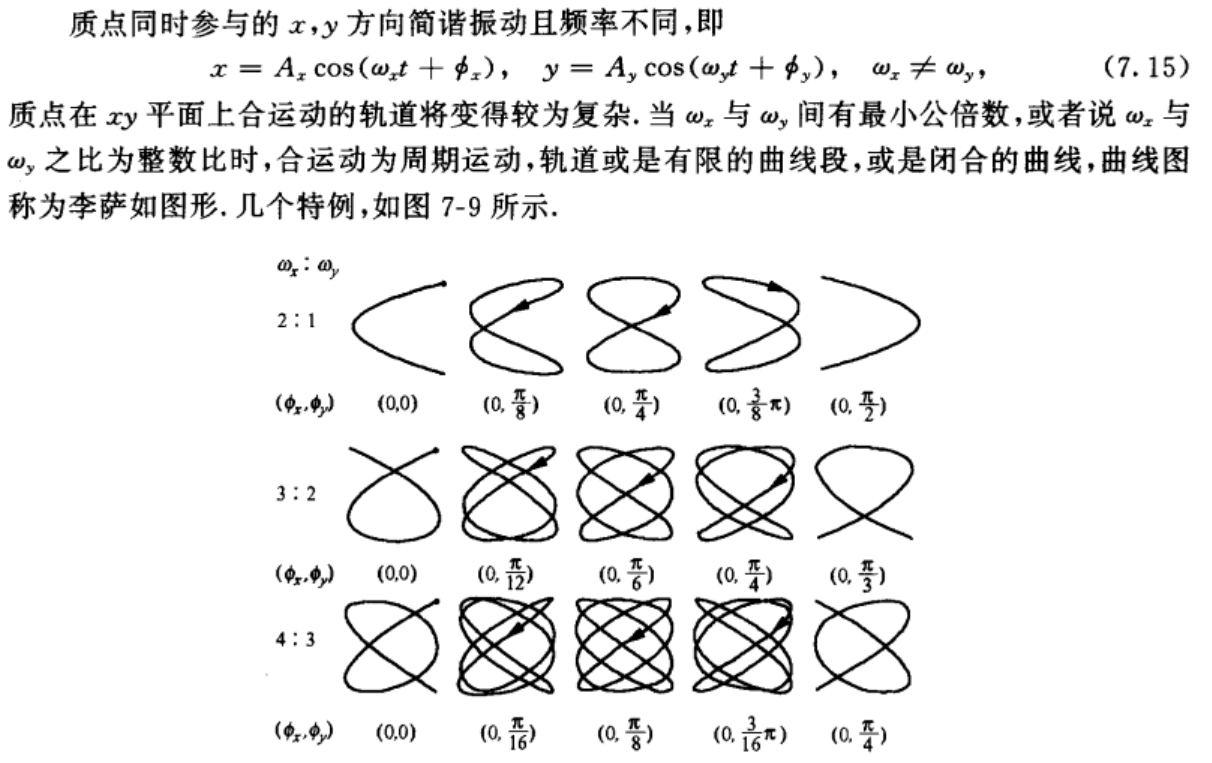
合成出来的可能性:圆、正/斜椭圆、直线段
一般的情况
\(x=A_xcos(\omega t+\phi_x)\)
\(y=A_ycos(\omega t+\phi_y)\)
\(\vec{r}=x\vec{i}+y\vec{j}\),这个就是运动轨迹
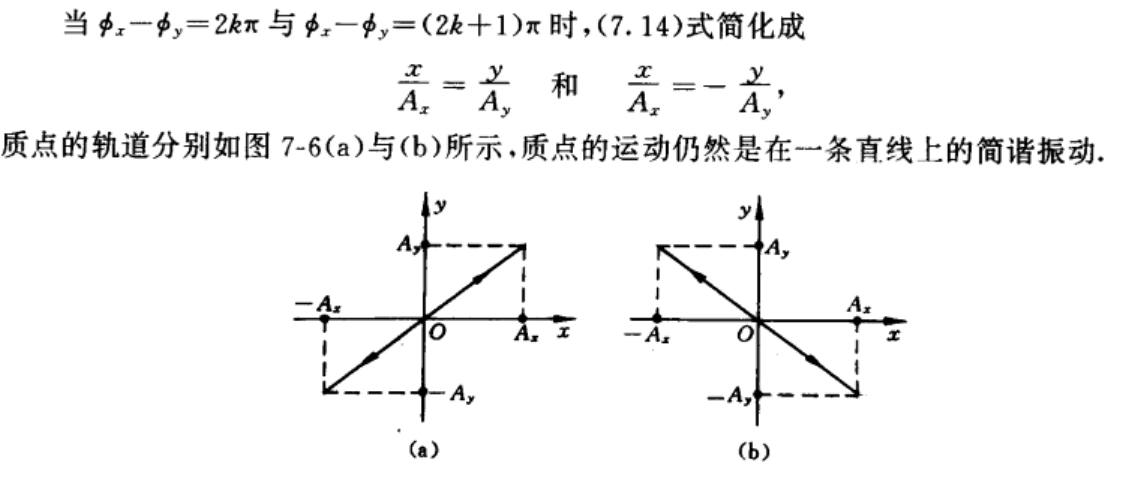
\(\frac{x^2}{A_x^2}+\frac{y^2}{A_y^2}-\frac{2}{A_xA_y}cos(\phi_x-\phi_y)=sin^2(\phi_x-\phi_y)\)
一般的运动轨迹是斜椭圆
正椭圆
如果\(\phi_x-\phi_y=(k+\frac{1}{2}\pi)\)
则\(\frac{x^2}{A_x^2}+\frac{y^2}{A_y^2}=1\),正椭圆
如果k=0或者k是一个偶数
这时x振动比y振动超前了\(\frac{\pi}{2}\),分别画出xy坐标与时间的关系,不难看出是逆时针旋转
如果k=-1(或者k是一个奇数)
这时y振动比x振动超前了\(\frac{\pi}{2}\),分别画出xy坐标与时间的关系,不难看出是顺时针旋转
线
垂直方向不同频率
非简谐振动的简谐分解
振动分为有周期T(T为有限量)和没有周期的。比如阻尼振动就没有周期。
有周期的振动
x(t+T)=x(t) 数学上有傅里叶级数展开


矢量表述
\(x=Acos(\omega t+\phi)\) 用圆周运动分运动来表述简谐运动,我们约定只画出t=0时的位置矢量,来进行简化。
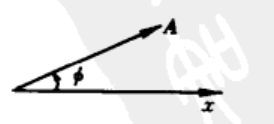
\(x(t)=\vec{A}(t)\cdot\vec{i}\) 注意\(\vec{i}\)是x轴方向向量
\(x_1=A_1cos(\omega t+\phi_1)\)
\(x_2=A_2cos(\omega t+\phi_2)\)
\(x=x_1+x_2=(\vec{A_1}(t)+\vec{A_2}(t))\cdot\vec{i}\)
引入\(\vec{A}=\vec{A_1}+\vec{A_2}\)
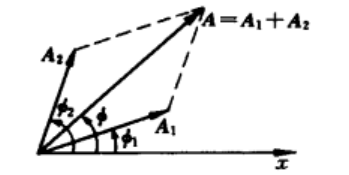
因为旋转角速度相同,所以可以用这种叠加代表任意时刻的
复数表述
\(x=Acos(\omega t+\phi)\)
\(y=Asin(\omega t+\phi)\)
y轴虚轴,x轴实轴
转化成一个复数\(A'(t)=x(t)+iy(t)\)
利用欧拉公式我们可以把它表述为复振动\(Ae^{i(\omega t+\phi)}\),实部是真实振动
对\(A'(t)\)求导得\(i\omega Ae^{i(\omega t+\phi)}\)发现实部就是真是振动的导函数
动力学内容
动力学方程
回顾运动学内容:
匀速圆周运动,x直径方向分运动的运动方程\(x=Acos(\omega t+\phi)\)
两边对t求二阶导,知道\(x''+\omega^2x=0\)
动力学考查:
\(F_x=\vec{F}\cdot\vec{i}=-m\omega^2\vec{r}\cdot\vec{i}=-m\omega^2x\)
我们把\(F_x\)写成mx''代入上面的等式,同样也可以得到动力学微分方程\(x''+\omega^2x=0\)
简谐运动的通解是\(x=Acos(\omega t+\phi)\) A和\(\phi\) 由初始条件所确定
\(x_0=Acos(\phi)\)
\(v_0=-\omega Asin\phi\)
\(A=\sqrt{x_0^2+\frac{v_0^2}{\omega^2}}\)
\(tan\phi=\frac{-v_0}{\omega x_0}\)
若\(tan\phi>0\), \(\phi\)可以在第一或第三象限
若\(tan\phi<0\), \(\phi\)可以在第二或第四象限
接下来可以利用\(x_0,v_0\)协助判定在第几象限
水平弹簧振子

劲度系数k,物体质量m。\(F_x=-kx=mx''\)
得出微分方程\(x''+\frac{k}{m}x=0\)
\(\omega=\sqrt{\frac{k}{m}}\) 具有动力学性质
\(\omega=\frac{2\pi}{T}\) 运动学性质
复摆
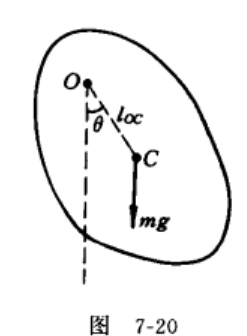
逆时针旋转为正方向,写出角动量定理:
\(M=I_o\beta\)
\(M=-mgsin\theta l_{oc}\) 负数,因为力矩方向指向纸面内
代入之后写出微分方程:\(\theta''+\frac{mgl_{oc}}{I_0}sin\theta\)
考虑小量近似\(sin\theta近似为\theta\)
于是\(\theta''+\omega^2\theta=0\)
\(\omega=\sqrt{\frac{mgl_{oc}}{I_0}}\)
与简谐振动数学上同构,因此\(\theta=\theta_0cos(\omega t+\phi)\)
特例:单摆
质量全集中在质心上就是单摆,此时\(I_o=ml_{oc}^2\)
此时\(\omega=\sqrt{\frac{g}{l}}\)
振动的能量
\(x=Acos(\omega t+\phi)\)
\(E_k=\frac{1}{2}m\omega^2A^2sin^2(\omega t+\phi)\)
\(E_p=\frac{1}{2}kx^2\)
可以看出\(E_p+E_k=\frac{1}{2}kA^2=E\)
简谐运动中E守恒:可以通过能量守恒求导后获得动力学微分方程
例子:复摆

\(E=E_k+E_p=\frac{1}{2}I_0\theta'^2+mgl_{OC}(1-ccos\theta)\)(注意,是\(\theta\)的导数)
两边求导,E守恒,因此左边为0
\(0=I_0\theta'\theta''+mgl_{oc}sin\theta \theta'\)
同样可以得到复摆动力学微分方程\(\theta''+\frac{mgl_{oc}}{I_0}sin\theta=0\)
保守力与势能
\(-dE_p=\vec{F}\cdot\vec{dl}\)
\(dE_p=\frac{\partial E_p}{\partial x}dx+\frac{\partial E_p}{\partial y}dy+\frac{\partial E_p}{\partial z}dz\)
\(\vec{F}\cdot\vec{dl}=F_xdx+F_ydy+F_zdz\)
\(-dE_p=\vec{F}\cdot\vec{dl}\)
于是\(F_x=-\frac{\partial E_p}{dx}\),\(F_y=-\frac{\partial E_p}{dy}\),\(F_z=-\frac{\partial E_p}{dz}\)
于是\(\vec{F}=-(\frac{\partial}{dx}\vec{i}+\frac{\partial}{dy}\vec{j}+\frac{\partial}{dz}\vec{k})E_p\)
引出哈密顿算符\(\nabla\)
\(\vec{F}=-\nabla E_p\)
把\(\nabla E_p\)成为\(E_p\)的梯度
阻尼振动
定义:除了恢复性的保守力(不损耗能量)之外,还有一个阻尼力(损耗能量),动能逐渐减小,有衰减现象,形成阻尼振动。
取\(F_x=-kx\),\(f_x=-\gamma x'\)
\(mx''=-kx-\gamma x'\)
\(x''+\frac{\gamma}{m}x'+\frac{k}{m}x=0\)
\(x''+2\beta x'+\omega_0^2x=0\)
\(\beta=\frac{\gamma}{2m}\) 阻尼系数
\(\omega_0=\sqrt{\frac{k}{m}}\) 本征/固有频率
三种解的情况
按照微分方程特征值正常讨论
(1)\(\beta>\omega_0\) 过阻尼
(2)\(\beta=\omega_0\) 临界阻尼
(3)\(\beta<\omega_0\) 低阻尼
\(x=Ae^{-\beta t}cos(\omega t+\phi)\)
\(\omega=\sqrt{\omega_0^2-\beta^2}\)
振动无周期,“振幅”随时间衰减
引入对数缩减\(\lambda\)

受迫振动
恢复性保守力+阻尼力+周期性变化的外力(策动力)
\(F_x=-kx\),\(f_x=-\gamma x'\),$F=F_0cost $
微分方程可以写出:
\(mx''+\gamma x'+\beta x=F_0cos\omega t\)
\(x''+2\beta x'+\omega_0^2 x=f_0 cos \omega t\)
\(\beta=\frac{\gamma}{2m}\) 阻尼系数
\(\omega_0=\sqrt{\frac{k}{m}}\) 本征/固有频率
\(f_0=\frac{F_0}{m}\)
微分方程找特殊解常常可以考虑\(x*=Acos(\omega t+\phi)\),\(A=\frac{f_0}{\sqrt{(\omega_0^2-\omega^2)+4\beta^2\omega^2}}\)
\(tan\phi=\frac{-2\beta \omega }{\omega_0^2-\omega^2}\)
三种解的情况
与阻尼振动的情况类似
低阻尼情况
\(x=e^{-\beta t}cos(\sqrt{\omega_0^2-\beta^2}+\phi_0)+Acos(\omega t+\phi)\) 暂态解
\(Acos(\omega t+\phi)\) 稳态解,与初始状态无关
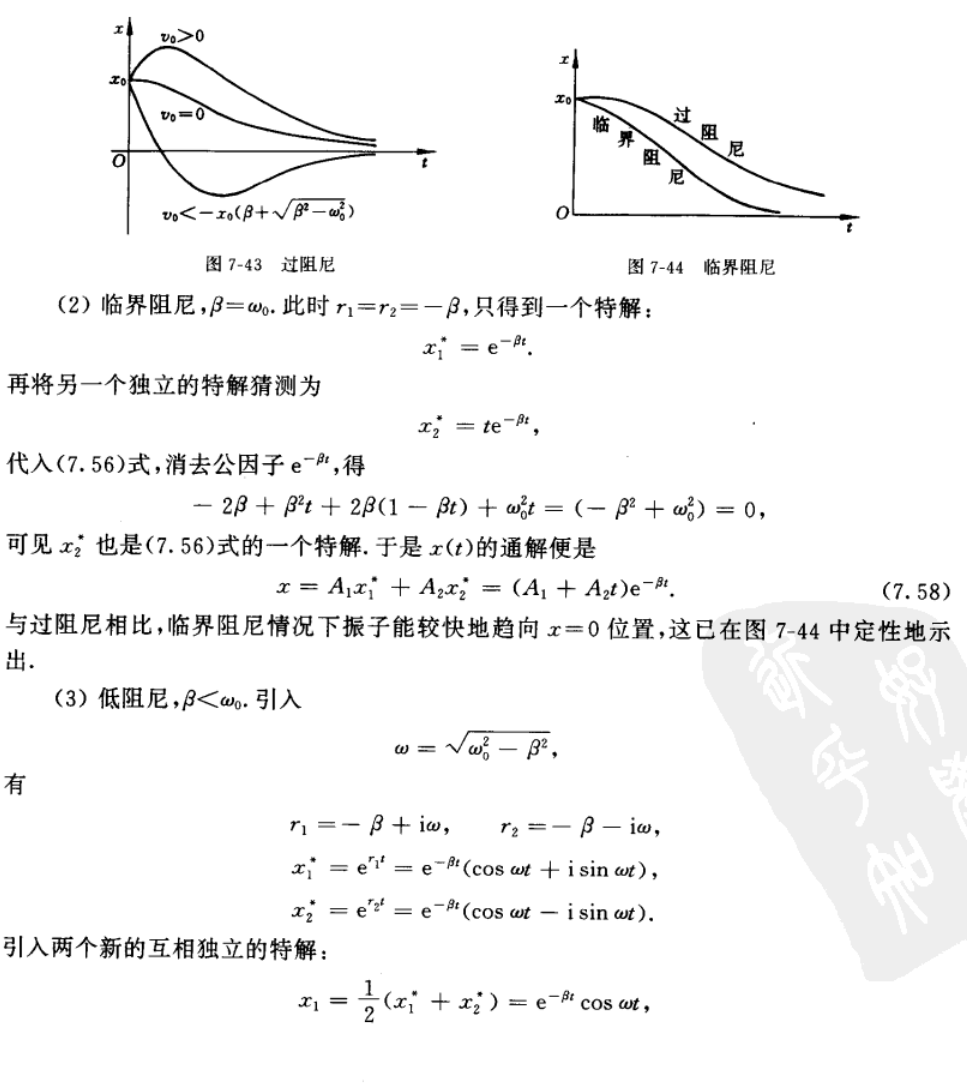
共振现象
条件:必须在低阻尼情况下讨论
给定\(\beta\) 讨论A与\(\omega\)的关系
当 \(\beta <\frac{\omega_0}{\sqrt{2}}\) 会出现振幅共振现象,即外加频率=固有频率时,振幅最大
波动现象
波是振动状态传播形成的物理现象
要素:波源、介质
分类
机械波(水波、地震波)、非机械波(电磁波)
简谐波、非简谐波
横波(水面波、线波、电磁波)、纵波(声波、长弹簧波);地震波既有横波也有纵波
线波、面波、空间波
空间波
分类
平面波、柱面波、球面波、其他

定义
波阵面:某时刻空间振动相位相同的点组成的面
波前:t时刻最前方的波阵面
波线:波的传播方向线
简谐波
平面简谐波
能量密度不变,因此A不变
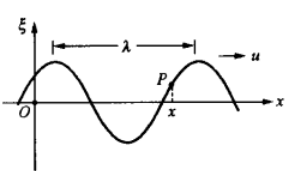
\(\xi=\xi(t,x)\)定义为振动量
波是振动状态的传播,而这个振动状态是简谐振动
于是只需要找x=0,\(\xi(t,x=0)=Acos(\omega t+\phi)\)
\(\xi(t,x)=\xi(t-\frac{x}{u},x=0)\)
u波速,\(\lambda\)波长
因此\(\xi(t,x)=Acos(\omega (t-+\frac{x}{u})+\phi)\)右传播-左传播+
\(\lambda=uT\)
\(\frac{\omega}{u}=\frac{2\pi}{\lambda}\)
于是\(\xi(t,x)=Acos(\omega t-+\frac{2\pi}{\lambda}x+\phi)\)右传播-左传播+,这种表示方式可以看出相对位置的影响
定义\(k=\frac{2\pi}{\lambda}\)为波数(可以理解为空间中的"角频率")
矢量化\(\vec{k}=k\vec{i}\)
于是\(\xi(t,x)=Acos(\omega t- \vec{k}\cdot\vec{x} +\phi)\)

球面简谐波
能量密度与\(r^2\)成反比,因此\(A_r\)与\(\frac{1}{r}\)成正比
\(\xi(r,t)=\frac{A}{r}cos(\omega t-\frac{2\pi}{\lambda}r+\phi)\) 注意这里的A并不是振幅
\(\xi(r,t)=\frac{r_0}{r}A_0cos(\omega t-\frac{2\pi}{\lambda}r+\phi)\) 这种表示方式可以给定一个位置的振幅,来求其他的振幅
波干涉与驻波
波的独立传播现象:若干列相同种类的波,在介质中传播的时候,如果动力方程是线性的,则每一列波的传播不受其他波列的影响。
波的叠加:满足上述现象的波,在空间每一个点形成的合振动即为各自独立存在时振动量的叠加。
干涉
相干波列:同频率,同振动方向,有固定的初相位或者有固定的初相位差。
相干波源:产生相干波列的波源。
波的干涉:相干波列在介质中各处合振动振幅有不随时间变化的空间分布。

特例:\(\phi_1-\phi_2=0\)
则\(r_2-r_1=k\lambda\) 有A最大值
\(r_2-r_1=k+\frac{1}{2}\lambda\) 有A最大值
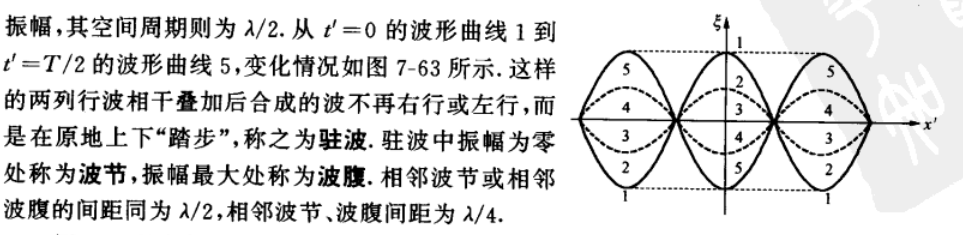
驻波
\(A_1=A_2=A\)
则最大振幅为2A,最小振幅为0
波的衍射反射折射
惠更斯原理
t时刻波前的每一个点部位都可以看作是产生球面子波的新波源,这些子波在\(t+\Delta t\)时刻波前的包络面就是整个波在\(t+\Delta t\)时刻的波前
折射定律
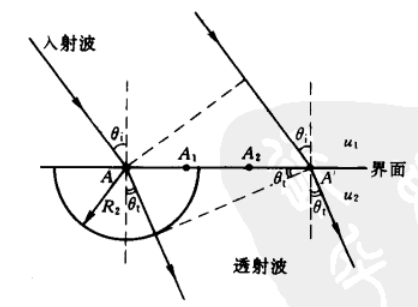
折射定律:\(\frac{u_1}{sin\theta_i}=\frac{u_2}{sin\theta_t}\)
反射定律
如果镜子不动,则反射角等于入射角
镜子向下运动,则反射角大于入射角
镜子向上运动,则反射角小于入射角
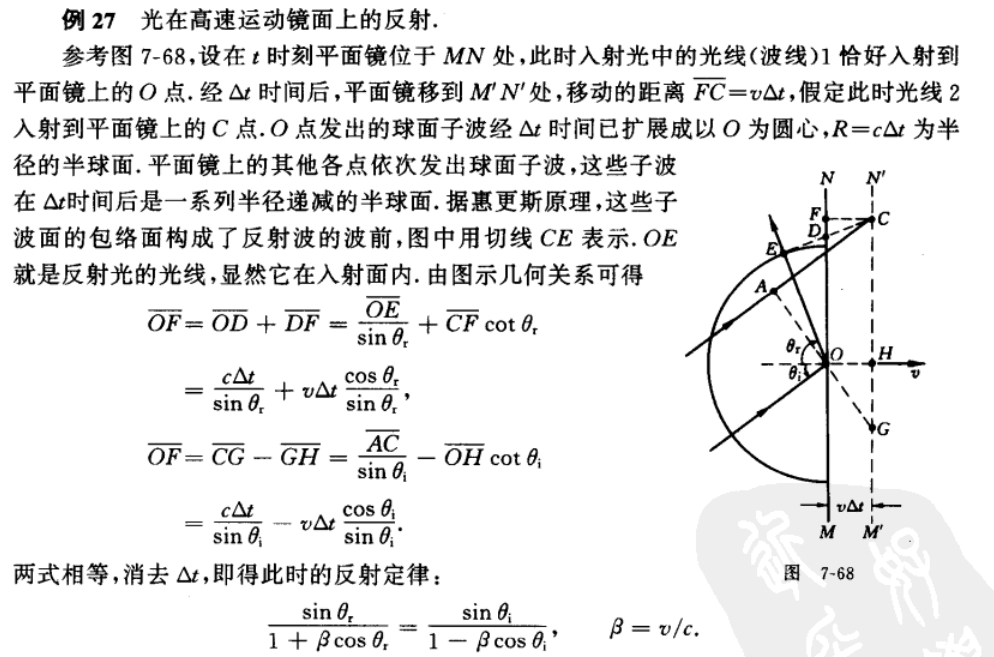
半波损失
假设遇上某一个介质分界面,只有反射没有透射。
反射有\(\pi\)相位突变,相当于减少半个波长。
多普勒效应
讨论相对接收者运动的波源
定义观测者B在单位时间内接收到的波列长度为u,其中包含波长个数即为单位时间内接收到的全振动次数,定义为接收频率。\(\nu=\frac{u}{\lambda}\)
都不动
显然\(\nu=\nu_0\)
S不动B动
假设B向S运动,则单位时间接收到波列长度为\(u+v_B\)
\(\nu=\frac{u+v_B}{\lambda_0}=\frac{u+v_B}{u}\nu_0\)
如果B背离S运动,则上述式子中的+改为-(要求\(v_B<u\))
注意如果\(v_B>u\)不属于多普勒效应
冲击波
\(v_B>u\)时是冲击波
\(sin\theta=\frac{u}{v}\)
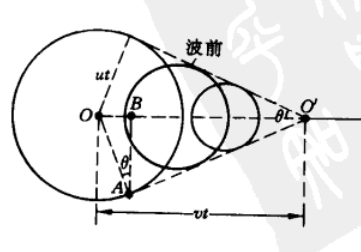
S动B不动
观测者认为波长改变了
假设B向S运动,\(\lambda'=\lambda_0-v_ST_0=(u-v_S)T_0\)
\(\nu=\frac{u}{\lambda'}=\frac{u}{u-v_S}\nu_0\)
如果B背离S运动,则上述式子中的-改为+
SB都动
\(\nu=\frac{u+-v_B}{u+-v_S}\)
一维线性波动方程
波动方程
平面简谐波:\(\xi(x,t)=Acos[\omega(t-\frac{x}{u})+\phi]\)
简谐振动动力学微分方程:\(x''+\omega^2x=0\)
\(\frac{\partial^2\xi}{\partial t^2}=-\omega^2\xi\)
\(\frac{\partial^2\xi}{\partial x^2}=-\frac{\omega^2}{u^2}\xi\)
\(\frac{\partial^2\xi}{\partial t^2}-u^2\frac{\partial^2\xi}{\partial x^2}=0\)
弹性介质中的纵波横波
波速
横波
取一小段弹簧dx,记它的伸长量为\(d\xi\)
弹性,则知道\(\frac{d\xi}{dx}\)与\(\frac{F}{S}\)成正比
\(E\frac{d\xi}{dx}=\frac{F}{S}\),E为常量,定义为杨氏模量
\(k_{dx}=\frac{F}{d\xi}=\frac{ES}{dx}\)(很小一段的伸长量)
\(k=\frac{ES}{l}\) 长度为l的弹性介质的劲度系数

假设匀质柱体密度为\(\rho\)初始长度为x
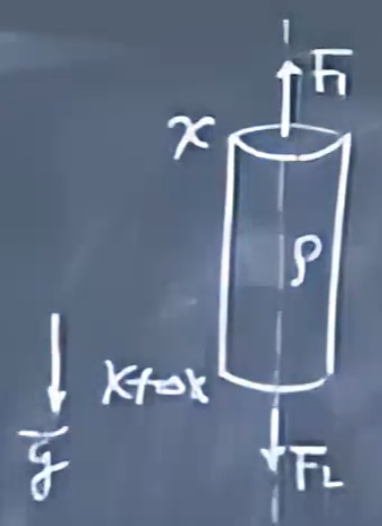
则\(\rho s \Delta x \frac{d^2\xi}{dt^2}=\rho s \Delta x g+F_2-F_1\)
\(F_1=ES(\frac{d\xi}{dx})_x\)
\(F_2=ES(\frac{d\xi}{dx})_{x+\Delta x}\)
代入把右边化简为二阶导再约分
\(\frac{d^2 \xi}{dt^2}-\frac{E}{\rho}\frac{d^2 \xi}{dx^2}=g\)
变成偏导得一阶线性非齐次方程
\(\frac{\partial^2 \xi}{\partial t^2}-\frac{E}{\rho}\frac{\partial^2 \xi}{\partial x^2}=g\)
如果改为水平放置,则\(\frac{\partial^2 \xi}{\partial t^2}-\frac{E}{\rho}\frac{\partial^2 \xi}{\partial x^2}=0\)
水平放置时\(u=\sqrt{\frac{E}{\rho}}\)
纵波
纵波波速:\(u=\sqrt{\frac{G}{\rho}}\)
线波

波动方程的解
\(\frac{\partial^2\xi}{\partial t^2}-u^2\frac{\partial^2\xi}{\partial x^2}=0\)
通解:设x=0为\(\xi(0,t)=\Phi(t)\)
右形波\(\xi(x,t)=\xi(0,t-\frac{x}{u})=\Phi(t-\frac{x}{u})\)
左形波\(\xi(x,t)=\xi(0,t+\frac{x}{u})=\Phi(t+\frac{x}{u})\)
通解:\(\xi(x,t)=\Phi_1(t-\frac{x}{u})+\Phi_2(t+\frac{x}{u})\)
如果引入t=0时各个x的振动量分布函数,表示为\(F_1(x)\)
再给出各个x振动的速度分布函数,表示为\(F_2(x)\)
则\(\Phi_1,\Phi_2\)函数形式由\(F_1(x)\)和\(F_2(x)\)确定
波的能量
弹性介质纵波为例取简谐波
\(\xi(x,t)=Acos[\omega(t-\frac{x}{u})+\phi]\)
为方便取\(\phi=0\)
取一段介质,面积dS,长度从x到x+dx,密度\(\rho\)
dV=dSdx
\(dE_k=\frac{1}{2}(\rho dS dx)(\frac{\partial \xi}{\partial t})^2\)
\(dE_k=\frac{1}{2}\rho \omega^2 A^2 sin^2[\omega(t-\frac{x}{u})]dsdx\)
\(dE_p=\frac{1}{2}k_{dx}[\xi(x+dx,t)-\xi(x,t)]^2\)
\(dE_p=\frac{1}{2}Edsdx(\frac{\partial \xi}{\partial x})^2\)
\(dE_p=\frac{1}{2}\rho \omega^2 A^2 sin^2[\omega(t-\frac{x}{u})]dsdx\)
发现一个重要规律:\(dE_p=dE_k\)
能量密度
\(\epsilon=\frac{dE}{dV}\) \(dE=dE_k+dE_p\)
\(\epsilon=\rho \omega^2 A^2 sin^2[\omega(t-\frac{x}{u})]\)
波场的能流密度
u是波的传播速度
\(i=\frac{dE}{ds dt}=\epsilon u\)
把它矢量化为\(\vec{i}=\epsilon \vec{u}\)
习题
题1

\(\omega=\sqrt{\frac{k}{m}}\)
\(T=\frac{2\pi}{\omega}\)
\(t=\frac{T}{4}\)
\(h+\Delta l=\frac{1}{2}gt^2\)
算出\(h=(\frac{\pi^2}{8}-1)\frac{M}{k}g\)
碰后粘连,讨论其后的运动
\(v_0=\frac{1}{2}(gt+\omega \Delta l)\) 注意,这个\(\Delta l\)也是振幅
因此\(v_0=\frac{1}{2}(1+\frac{\pi}{2})\sqrt{\frac{M}{k}}g\)
把碰上的时刻看成t=0时刻。新的力平衡位置要再下移\(\Delta l\)
建立向下的坐标,取新的平衡位置为坐标原点,取向下为正方向
\(y=Acos(\omega't+\phi)\)
\(\omega'=\sqrt{\frac{k}{2M}}\)
t=0时,\(y_0=-\Delta l\)
用公式\(A=\sqrt{y_0^2+\frac{v_0^2}{\omega^2}}=\sqrt{1+\frac{1}{2}(1+\frac{\pi}{2})^2}\sqrt{\frac{M}{k}}g\)
A大约2.07\(\frac{Mg}{k}>2\frac{Mg}{k}\) 因此并不是纯粹的简谐振动
\(tan\phi=\frac{1}{\sqrt{2}}(1+\frac{\pi}{2})>0\)
又由于\(y_0=Acos\phi\)是负的,可以确定\(\phi\)是第三象限
\(\phi=\pi+arctan(\frac{1}{\sqrt{2}}(1+\frac{\pi}{2}))\)
题2

重点:碰之后B和B'的质心匀速直线运动,B相对于质心简谐运动

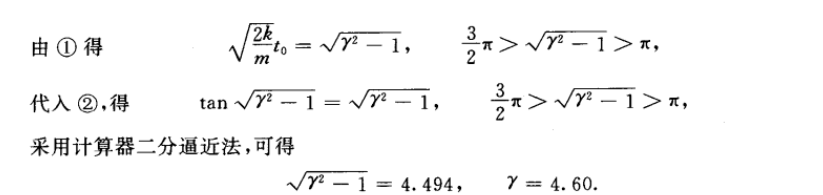
题3

纯滚动,静摩擦力做功为零,因此机械能守恒
\(E=\frac{1}{2}mv_c^2+\frac{1}{2}I_c+mg(R-r)(1-cos\theta)\)
\(v_c=(R-r)\theta '\)
\(\phi'=(\frac{R}{r}-1)\theta\)
把方程两边对t求导,并取小角度近似\(sin\theta=\theta\)
\(\theta''+\frac{5g}{7(R-r)}\theta=0\)