多元函数微分

计算内容

求极限：二重极限，累次极限

函数连续性、可微性的判断

全微分计算

方向导数的计算

二重极限

考查函数的连续性计算的就是二重极限，二重极限可以理解为x,y两个变量同时趋于某一点。当然，趋于某一点的路径是随意的。在证伪时，路径的多样性是一个很好的工具。

存在

放缩

此方法适用于证明/求解极限为0者。最终利用的是\(\rho→0\),或者是x→0且y→0

均值不等式

\(\lim_{(x,y)→(0,0)}\frac{x^2y^2}{x^2+y^2}\)

\(\frac{x^2y^2}{x^2+y^2} \leq \frac{x^4+y^4}{2(x^2+y^2)}\leq \frac{1}{2}\frac{x^2}{x^2+y^2}x^2+\frac{1}{2}\frac{y^2}{x^2+y^2}y^2\leq \frac{1}{2}(x^2+y^2)\)

趋于0，证毕

中值定理

\(\frac{e^{x^3+y^3}-1}{x^2+y^2}\)在(0,0)处的极限是否存在？

\(e^{x^3+y^3}-e^0=e^\epsilon (x^3+y^3)\) 注意\(\epsilon \in (0,1)\)

$||e||e(|x|+|y|) e(|x|+|y|) $

趋于0，证毕

分离绝对值或平方

上面的两道例题也用了这个方法，我们可以各提取出一个x,y的平方或者绝对值，然后把剩下的直接放大到1

设 [ f(x, y)= \[\begin{cases} \frac{x^{2}+y^{2}}{\vert x\vert+\vert y\vert}, & (x, y)\neq(0, 0)\\ 0, & (x, y)=(0, 0) \end{cases}\]

] 证明函数 \(f\) 在原点 \((0, 0)\) 处连续。

[ \[\begin{align*} \vert f(x, y)-f(0, 0)\vert&=\frac{x^{2}+y^{2}}{\vert x\vert+\vert y\vert}\\ &=\vert x\vert\frac{\vert x\vert}{\vert x\vert+\vert y\vert}+\vert y\vert\frac{\vert y\vert}{\vert x\vert+\vert y\vert}\leq\vert x\vert+\vert y\vert \end{align*}\] ]

因此当 \(\|(x, y)-(0, 0)\|=\sqrt{x^{2}+y^{2}}\) 充分小时，\(\vert f(x, y)-f(0, 0)\vert\) 可以任意小。故 \(\lim_{(x, y)\to(0, 0)}f(x, y)=f(0, 0)\)。这就证明了函数 \(f(x, y)\) 在原点 \((0, 0)\) 处连续。命题得证。

整体看

\(\lim_{(x,y)→(0,0)}\frac{xy-sin(xy)}{xy-cos(xy)}\)

直接xy=u，泰勒即可，答案三分之一

分而治之

\(\lim_{(x,y)→(0,0)}(x+1)^\frac{1+y}{xy}\)

\(\frac{1}{x+1}\frac{x+1}{x}\frac{1+y}{y}\) 如此拆分指数部分即可

得出最终的极限为\(e^1=e\)

不存在

两种思想。要么找一条特殊路径让极限不存在，要么找俩路径极限存在但不等。

正比例函数

此方法适用于否定齐次函数的极限

eg.\(\lim_{(x,y)→(0,0)}\frac{x^2-y^2}{x^2+y^2}\)

从y=kx趋近，极限为\(\frac{1-k^2}{1+k^2}\)，取不同的k极限存在但不相等。

二次函数

这个适用的类型类似于上面的齐次函数

\(\lim_{(x,y)→(0,0)}\frac{x^2y}{x^4+y^2}\)

取\(y=kx^2\)趋近，则极限为\(\frac{k}{1+k^2}\)

累次极限

对于二元的就是二次极限，每一次求极限都只取一个变量，剩下是常量。当然，只有前一个极限存在才能继续算下一个。

例子

设 \(f(x, y)=\frac{x^2 - y^2}{x^2 + y^2}\)，其定义域为 \(D = \mathbb{R}^2\setminus\{(0, 0)\}\)。之前已证，函数 \(f(x, y)\) 在点 \((0, 0)\) 处的全面极限不存在。现考察累次极限。不难证明

\[ \lim_{y \to 0}\lim_{x \to 0}f(x, y)=\lim_{y \to 0}\frac{-y^2}{y^2}=-1. \] \[ \lim_{x \to 0}\lim_{y \to 0}f(x, y)=\lim_{x \to 0}\frac{x^2}{x^2}=1. \]

累次极限与重极限

定理：

1. 若以下三个极限均存在 \[\lim_{y \to y_0}\lim_{x \to x_0}f(x, y), \lim_{x \to x_0}\lim_{y \to y_0}f(x, y), \lim_{(x, y)\to(x_0, y_0)}f(x, y),\] 则它们的极限值均相等；

2. 若两个累次极限存在，但极限值不等，则重极限不存在。

可微与偏导

定义：记二元函数 \(f(x, y)\) 定义域为 \(D\)，设点 \((x_0, y_0)\) 是 \(D\) 的一个内点。若存在两个数 \(\lambda, \mu \in \mathbb{R}\)，使得对 \(\forall h, k \in (-\delta, \delta)\)， [ f(x_0 + h, y_0 + k) - f(x_0, y_0) - (h + k) = o(), ] 则称函数 \(f(x, y)\) 在点 \((x_0, y_0)\) 处可微，并称线性函数 \(\lambda h + \mu k\) 为 \(f(x, y)\) 在点 \((x_0, y_0)\) 处的微分，记作 \(\left.\mathrm{d}f\right|_{(x_0,y_0)} = \lambda h + \mu k\)。自变量 \(x, y\) 的增量 \(h, k\) 常写作 \(h = \Delta x, k = \Delta y\)。故微分常写作 \(\left.\mathrm{d}f\right|_{(x_0,y_0)} = \lambda\Delta x + \mu\Delta y\)。

微分是唯一的,也就是说\(\lambda ,\mu\)是唯一的。其中\(\lambda=\frac{\partial f}{\partial x}\) \(\mu=\frac{\partial f}{\partial y}\)

可微→

如果一个函数在某一点可微，那么.....?

1、函数在这一点连续

2、在这一点沿着任意方向的方向导数均存在，当然偏导数也存在。

（偏导数不存在一定不可微）

注意:偏导数存在不能推出连续，更不能推出可微。

考虑函数 [ f(x, y)= \[\begin{cases} 0, & xy = 0\\ 1, & xy \neq 0 \end{cases}\]

] 显然函数 \(f\) 在原点处不连续。但 \(f\) 在原点的两个偏导数存在。因为 [ ==0, x ] 这说明偏导数 \(f_x(0, 0)\) 存在，且 \(f_x(0, 0)=0\)。同理可证偏导数 \(f_y(0, 0)\) 存在，且 \(f_y(0, 0)=0\)。

判断是否可微

首先看偏导是否存在，偏导数不存在就不可微。

然后计算[_{→0} ]

\(\rho=\sqrt{h^2+k^2}\)

高阶偏导

n阶偏导有\(2^n\)个高阶偏导。感觉高阶偏导和累次极限有点像。

\(\frac{\partial^2 f}{\partial x^2}=f_{xx}=D_{xx}f\)

\(\frac{\partial ^2 f}{\partial y\partial x }=f_{xy}=D_{xy}f\)

Clairaut定理

设\(f(x, y)\)在开区域\(D \subset \mathbb{R}^2\)上定义。假设两个二阶混合偏导数\(f_{xy}(x, y)\)和\(f_{yx}(x, y)\)在\(D\)上处处存在，且在点\((x_0, y_0)\)处均连续，则\(f_{xy}(x_0, y_0) = f_{yx}(x_0, y_0)\)。

证明思路大概是累次极限+中值定理，最后利用连续性。

Clairaut定理断言，如果

1. 两个混合偏导数 \(f_{xy}, f_{yx}\) 在开区域 \(D\) 上存在；

2. \(f_{xy}\) 和 \(f_{yx}\) 在点 \((x_0, y_0)\) 处均连续

则 \(f_{xy}(x_0, y_0) = f_{yx}(x_0, y_0)\)。

条件 (ii) 可减弱为 (ii)' \(f_{xy}\) 或 \(f_{yx}\) 在点 \((x_0, y_0)\) 处连续。

\(f_{xy}\)≠\(f_{yx}\)

(课本第40页例1.4.16.) 设 [ f(x, y)= \[\begin{cases} \frac{xy(x^{2}-y^{2})}{x^{2}+y^{2}}, & (x, y)\neq(0, 0)\\ 0, & (x, y)=(0, 0) \end{cases}\]

]

考虑 (f(x, y)) 的两个二阶混合偏导数 (f_{xy}) 和 (f_{yx})。判断 (f_{xy}(0, 0)) 和 (f_{yx}(0, 0)) 是否存在。存在时求出它们的值。

解答：

在开区域 (^2{(0, 0)}) 上，(f(x, y)) 是分式函数，故它的各阶偏导数均连续。计算得它的一阶和二阶混合偏导数如下 [ f_x(x, y)=, f_y(x, y)=, ] [ f_{xy}(x, y)= = f_{yx}(x, y). ]

不难看出 (f_{xy}, f_{yx}) 在点 ((0,0)) 处的极限都不存在. (因为它们沿着两个坐标轴趋于 ((0,0)) 时有极限 (1) 和 (-1).) 因此二阶混合偏导在点 ((0,0)) 处均不连续.

！但这并不表明 (f_{xy}(0, 0), f_{yx}(0, 0)) 不存在！

以下考虑它们的存在性与计算. 由于 [ ==0 , (x ). ] 故 (f_x(0,0)) 存在且 (f_x(0,0)=0). 同理可证 (f_y(0,0)) 存在且 (f_y(0,0)=0). 由于 [ ==-1 , (y ), ] 这说明 (f_{xy}(0,0)) 存在且 (f_{xy}(0,0)= -1). 类似地, 由于 [ ==1 , (x ), ] 故 (f_{yx}(0,0)) 存在, 且 (f_{yx}(0,0)= 1 = f_{xy}(0,0)). 解答完毕.

方向导数

定义

f(x,y)的定义域包含点\(z_0\)=\((x_0,y_0)\)的一个领域，u=(a,b)为一个单位向量，往下称单位向量u为一个方向。若极限\(\lim_{t→0}\frac{f(z_0+tu)-f(z_0)}{t}=\lim_{t→0}\frac{f(x_0+ta,y_0+tb)-f(x_0,y_0)}{t}\)存在，则称之为函数f再点\(z_0\)处沿着方向u的导数。

记作\(\frac{\partial f}{\partial u}(x_0,y-0)\)或者\(D_uf|_{(x_0,y_0)}\)

几何意义

偏导数就是一种特殊的方向导数

计算

偏导数=梯度与方向的内积

$D_uf(x,y)=f(x,y)u $

\(\nabla f(x_1,x_2,x_3,...)=(\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2},\frac{\partial f}{\partial x_3})\)

注意这里求梯度代入的点就是趋近于的点

梯度的性质

1. 常数函数的梯度为零，即 \(\nabla c = 0\)；

2. \(\nabla(\lambda f)=\lambda\nabla f\)，\(\lambda\) 为常数；

3. \(\nabla(f\pm g)=\nabla f\pm\nabla g\)；

4. \(\nabla(fg)=g\nabla f + f\nabla g\)；

5. \(\nabla(f/g)=\frac{1}{g^2}(g\nabla f - f\nabla g)\)，\(g\neq 0\)；

6. \(\nabla u(f)=u'(f)\nabla f\)，这里 \(u(t)\) 为一元可微函数。

最值

定理：设函数 \(f(x)\) 在点 \(x_0\) 处可微，且 \(\nabla f(x_0) \neq 0\)，则函数 \(f(x)\) 沿着梯度方向 \(\nabla f(x_0)/\|\nabla f(x_0)\|\) 可取得方向导数的最大值，且最大值为 \(\|\nabla f(x_0)\|\)；沿负梯度方向 \(-\nabla f(x_0)/\|\nabla f(x_0)\|\) 取得方向导数值最小值且最小值为 \(-\|\nabla f(x_0)\|\)。

证明很简单，两个向量的内积同方向达到最大，反向则最小。

例题

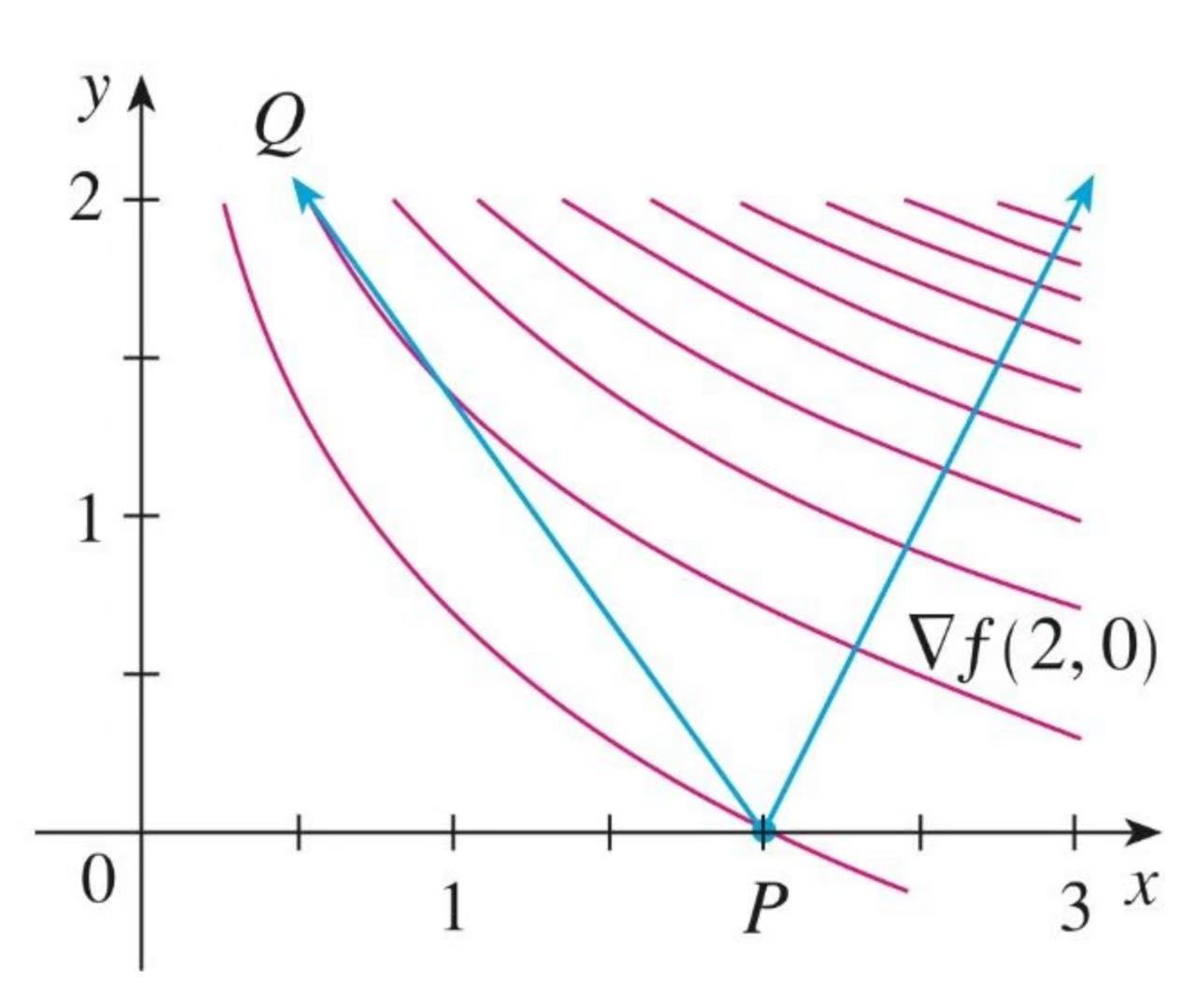
设 \(f(x, y)=xe^y\)。

1. 求函数在点 \(P = (2, 0)\) 处，沿着方向 \(\overrightarrow{PQ}\) 的方向导数，这里 \(Q=(0.5, 2)\)；

2. 求函数在点 \(P\) 处的方向导数的最大值。

简单计算得 \(\nabla f(x, y)=(e^y, xe^y)\)，\(\nabla f(2, 0)=(1, 2)\)。

1. 计算 \(\overrightarrow{PQ}=(0.5, 2)-(2, 0)=(-1.5, 2)\)，其单位向量为 \(u = (-\frac{3}{5}, \frac{4}{5})\)。

故函数在点 \(P = (2, 0)\) 处沿着方向 \(u\) 的方向导数为 \(D_uf(2, 0)=\nabla f(2, 0)\cdot u=(1, 2)\cdot(-\frac{3}{5}, \frac{4}{5}) = 1\)

2. 由定理知，函数在点 \(P\) 处沿着梯度方向 \(\nabla f(2, 0)=(1, 2)\) 的方向导数可取得最大值 \(\|\nabla f(2, 0)\|=\sqrt{5}\)。图示如下。

水平线（补充）

定义：对二元函数 \(f(x, y)\)，称集合 \(\{(x, y) \in D, f(x, y)=k\}\) 为函数 \(f\) 的水平线，或简单地说 \(f(x, y)=k\) 是水平线，这里 \(k \in \mathbb{R}\)，\(D \subset \mathbb{R}^2\) 是函数 \(f\) 的定义域。

例：考虑函数 \(f(x, y)=4x^2 + y^2\)。对于任意正数 \(k>0\)，水平线 \(4x^2 + y^2=k\) 为椭圆，其标准形式为

\[\frac{x^2}{k/4}+\frac{y^2}{k}=1,\]

两个半轴的长度分别为 \(\sqrt{k}/2\)，\(\sqrt{k}\)。函数图像及其水平线如下。

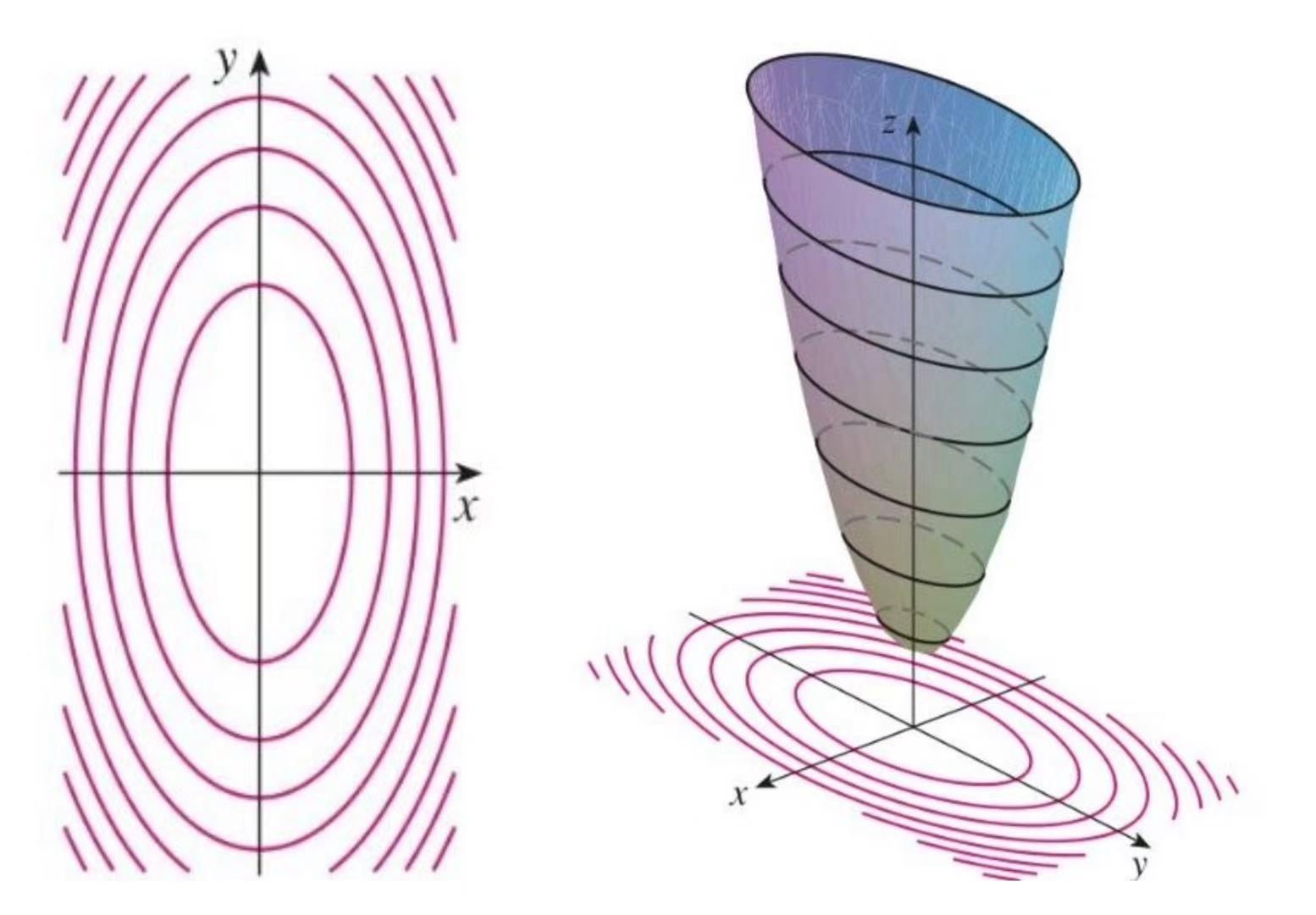
对于二元函数是水平线，如果推广到三元就是水平面了。

Jacobian 矩阵

设 ( f = (f_1, , f_m) ): ( D ^n ^m ) 为向量值函数，( D ) 为开集，( x_0 D )，则：

1. ( f ) 在点 ( x_0 ) 处可微 () 每个分量函数 ( f_i ) 在点 ( x_0 ) 处可微；
2. 当 ( f ) 在点 ( x_0 ) 处可微时，( f'(x_0) ) 可表示为：

[ f'(x_0) = \[\begin{bmatrix} \frac{\partial f_1}{\partial x_1} & \frac{\partial f_1}{\partial x_2} & \cdots & \frac{\partial f_1}{\partial x_n} \\ \frac{\partial f_2}{\partial x_1} & \frac{\partial f_2}{\partial x_2} & \cdots & \frac{\partial f_2}{\partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial f_m}{\partial x_1} & \frac{\partial f_m}{\partial x_2} & \cdots & \frac{\partial f_m}{\partial x_n} \end{bmatrix}\]

_{x_0} ]

上述矩阵 ( f'(x_0) ) 称为映射 ( f ) 在点 ( x_0 ) 处的 Jacobian 矩阵。当 ( m = n ) 时，Jacobian 矩阵是方阵，其行列式称为 Jacobian 行列式。

例子

称二维映射 ( F: ^2 ^2 )， [ (r, ) (r, r) ] 为极坐标映射，其中： [ = {(r, ) r > 0, (0, 2) }. ] 映射在点 ( (r, ) ) 处的 Jacobian 矩阵 为：

[ DF(r, ) = \[\begin{bmatrix} \cos\theta & -r\sin\theta \\ \sin\theta & r\cos\theta \end{bmatrix}\]

, ]

注：\(cos\theta\)是\(rcos\theta\)对x求导，\(-rsin\theta\)是\(rcos\theta\)对\(\theta\)求导。

\(A_{ij}=\frac{\partial f_i}{\partial x_j}\)

其 Jacobian 行列式 为： [ DF(r, ) = r > 0. ]

锁链规则

二元函数

定理：设二元函数\(f(x, y)\)，以及两个一元函数\(x(t), y(t)\)均可微，\(t \in J\)，且它们可以复合，则复合函数\(f(x(t), y(t))\)也可微，且 [ [f(x(t), y(t))]' = f_x(x, y)x'(t) + f_y(x, y)y'(t), ] 其中\((x, y) = (x(t), y(t)), t \in J\)。

多元函数

定理：设\(n\)元函数\(f(u_1, \cdots, u_n)\)在开集\(D \subset \mathbb{R}^n\)上为\(C^1\)的，映射\(u: J \subset \mathbb{R}^1 \to \mathbb{R}^n\)是\(C^1\)的，\(u = (u_1, \cdots, u_n)\)，且\(u(t) \in D, \forall t \in J\)，这里\(J\)为一个开区间，则复合函数\(f(u(t))\)在\(J\)上也是\(C^1\)的，且 [ [f(u_1(t), , u_n(t))]' = u_1'(t) + + u_n'(t), ] 或简写为\([f(u(t))]' = \nabla f(u) \cdot u'(t)\)，其中\(u = u(t), t \in J\)。

例题

课本第50页例1.5.4

设\(z = u^2v - uv^2\)，\(u = x\sin y\)，\(v = x\cos y\)，求偏导数\(z_x\)。

解： 记\(f(u, v) = u^2v - uv^2\)，则\(z = f(u, v)\)。根据上述定理可知 [ \[\begin{align*} z_x &= f_u(u, v)u_x + f_v(u, v)v_x = (2uv - v^2)u_x + (u^2 - 2uv)v_x\\ &= x^2[(2\cos y\sin y - \cos^2y)\sin y + (\sin^2y - 2\sin y\cos y)\cos y]\\ &= x^2[(\sin 2y - \cos^2y)\sin y + (\sin^2y - \sin 2y)\cos y]\\ &= \frac{3x^2}{2}\sin 2y(\sin y - \cos y) \end{align*}\] ]

例题2

设\(f(x, y)\)在全平面\(\mathbb{R}^2\)上连续可微，且\(f(x, x^2) \equiv 1, \forall x \in \mathbb{R}\)。

1. 若\(f_x(x, x^2) \equiv x, \forall x \in \mathbb{R}\)，求\(f_y(x, x^2)\)

2. 若\(f_y(x, y) \equiv x^2 + 2y, \forall (x, y) \in \mathbb{R}^2\)，求\(f(x, y)\)。

注：符号\(f_x(x, x^2)\)表示偏导数\(f_x(x, y)\)在抛物线\(y = x^2\)上取值，即\(f_x(x, x^2)= f_x(x, y)|_{y = x^2}\)。符号\(f_y(x, x^2)\)的意义类似。

解： (i) 对恒等式\(f(x, x^2) \equiv 1\)两边求导得\(f_x(x, x^2) + f_y(x, x^2)2x \equiv 0\)。若\(f_x(x, x^2) \equiv x\)，则\(x + 2xf_y(x, x^2) \equiv 0, \forall x \in \mathbb{R}\)。约去因子\(x\)得\(1 + 2f_y(x, x^2)\equiv 0\)。由此可得\(f_y(x, x^2) = -\frac{1}{2}, \forall x \in \mathbb{R}\)。

2. 令\(F(x, y) = f(x, y) - (x^2y + y^2)\)【为了构造\(F_y(x,y)=0\)】

则\(F(x, y)\)在\(\mathbb{R}^2\)上连续可微，且\(F_y(x, y)= f_y(x, y) - (x^2 + 2y) = 0, \forall (x, y) \in \mathbb{R}^2\)。故\(F(x, y)\)在\(\mathbb{R}^2\)上与变量\(y\)无关，即\(F(x, y) = \phi(x), \forall (x, y) \in \mathbb{R}^2\)，亦即\(f(x, y) = x^2y + y^2 + \phi(x)\)。

由假设\(f(x, x^2) \equiv 1\)可知\(x^2 \cdot x^2 + x^4 + \phi(x) \equiv 1\)，即\(\phi(x) = 1 - 2x^4\)。因此\(f(x, y)= x^2y + y^2 + 1 - 2x^4\)。解答完毕。

隐函数定理IFT

二元情形

设二元函数\(F(x, y)\)在平面开集\(D \subset \mathbb{R}^2\)上是\(C^1\)的。假设\(F(x_0, y_0) = 0\)且\(F_y(x_0, y_0) \neq 0\)，\((x_0, y_0) \in D\)，则存在唯一的 (隐) 函数\(f: J_{\alpha} \to J'_{\beta}\)，其中\(J_{\alpha} \triangleq (x_0 - \alpha, x_0 + \alpha)\)，\(J'_{\beta} \triangleq (y_0 - \beta, y_0 + \beta)\)，使得

1. \(y_0 = f(x_0)\)，\(F(x, f(x)) \equiv 0\)，\(\forall x \in J_{\alpha}\)；

2. 对于\((x, y) \in J_{\alpha} \times J'_{\beta}\)，\(F(x, y) = 0\)当且仅当\(y = f(x)\)；

3. 隐函数\(f(x)\)是\(C^1\)的，且 [ f'(x) = -.|{y = f(x)}, x J{} ]

多元情形

设\(F(x, y)\)为\(m + 1\)个变量\(C^1\)函数，定义域\(D \subset \mathbb{R}^{m + 1}\)为开集，这里\(x = (x_1, \cdots, x_m) \in \mathbb{R}^m\)，\(y \in \mathbb{R}\)。假设在点\((x_0, y_0) \in D\)处，\(F(x_0, y_0) = 0\)且\(F_y(x_0, y_0) \neq 0\)，则\(\exists\varepsilon, \delta > 0\)以及函数\(f(x)\)，\(x \in B_{\delta}(x_0)\)，使得

1. \(y_0 = f(x_0)\)，\(F(x, f(x)) \equiv 0\)，\(\forall x \in B_{\delta}(x_0)\)；

2. \(F(x, y) = 0\)当且仅当\(y = f(x)\)，\(\forall (x, y) \in B_{\delta}(x_0) \times J_{\varepsilon}(y_0)\)，这里\(J_{\varepsilon}(y_0)=(y_0 - \varepsilon, y_0 + \varepsilon)\)；

3. \(f(x)\)是\(C^1\)的，且\(\nabla f(x) = -F_y(x, y)^{-1}\nabla_xF(x, y)\big|_{y = f(x)}\)，\(x \in B_{\delta}(x_0)\)。

太长不看

隐函数问题是在探讨能不能通过方程F(x,y)=0写出来y(x)(或者x(y))。比如我们想要写出y(x),就要求每一个x有唯一的y与之对应。这样就需要F(x,y)在某一个区间内关于y单调变化，这样就可以唯一地解出来y(x)了。因此我们需要\(F_y(x,y)\neq 0\)，即每一个x对应唯一的y(局部)。

反函数定理

这个定理很直观，函数在某个区间单调可以写出反函数。实际上它就是隐函数定理的特殊化版本。

Theorem

设\(f(x)\)在开区间\((a, b)\)上连续可微。若\(f'(x_0) \neq 0\)，\(x_0 \in (a, b)\)，则存在\(\delta > 0\)，以及函数\(x = g(y)\)，\(y \in J\)，其中\(J = (y_0 - \delta, y_0 + \delta)\)，\(y_0 = f(x_0)\)，使得

1. \(x_0 = g(y_0)\)；

2. 当\(|x - x_0|\)和\(|y - y_0|\)均充分小时，\(y = f(x) \Longleftrightarrow x = g(y)\)；

3. \(g(y)\)在\(J\)连续可微，且 [ g'(y)=.|_{x = g(y)}, y J ]

Proof

证：记\(F(x, y) = y - f(x)\)，则\(F(x, y)\)是\(C^1\)的，\(F(x_0, y_0) = 0\)，且\(F_x(x_0, y_0)= -f'(x_0) \neq 0\)。故由IFT（隐函数定理，Implicit Function Theorem）知存在\(\varepsilon, \delta > 0\)，以及函数\(x = g(y)\)，\(y \in J\)，其中\(J = (y_0 - \delta, y_0 + \delta)\)，使得 (i) \(x_0 = g(y_0)\)； (ii) \(y = f(x) \Longleftrightarrow x = g(y)\)，\((x, y) \in K \times J\)，\(K = (x_0 - \varepsilon, x_0 + \varepsilon)\)； (iii) 函数\(x = g(y)\)是\(C^1\)的，且 [ g'(y)=-.|{x = g(y)}=.|{x = g(y)}, y J ]

定理得证。

做题的时候分两步，先找到F(x,y),然后判断需不需要用“存在隐函数”这个条件进行推导，还是说直接把隐函数看成一个“结果”。

用它作为“条件”

考虑下列方程，指出在哪些点处方程确定了隐函数\(y = y(x)\)或\(x = x(y)\)等。 \(e^{-(x + y+z)} = x + y + z\).

\(F(x,y,z)=e^{-(x + y+z)} - (x + y + z)\)

y=y(x)存在：\(F_y=-e^{-(x + y+z)} -1\) 恒小于0

x=x(y)存在:\(F_x=-e^{-(x + y+z)} -1\) 恒小于0

因此整个平面上都可以确定y(x)和x(y)。

看成“结果”

设\(f(u, v)\)可微，且有方程\(f(ax - cz, ay - bz) = 0\)确定了一个可微的隐函数\(z = z(x, y)\)，求\(cz_x + bz_y\);

\(f_x=f_uu_x+f_vv_x=f_u(a-cz_x)+f_v(-bz_x)=0\) 得出\(z_x=\frac{af_u}{cf_u+bf_v}\)

类似可以解出\(f_y\)，容易验证。

一般情形

设映射\(F(x, y)\)在\(\Omega\)上是\(C^1\)的，\(F(x_0, y_0) = 0\)且\(m\)阶矩阵\(F_y(x_0, y_0)\)非奇，则存在\(\varepsilon, \delta > 0\)，以及映射\(\phi(\cdot): B_{\delta}(x_0) \to \mathbb{R}^m\)，使得 (i) \(y_0 = \phi(x_0)\)； (ii) \(F(x, \phi(x)) \equiv 0\)，\(\forall x \in B_{\delta}(x_0)\)； (iii) 对于\((x, y) \in B_{\delta}(x_0) \times B_{\varepsilon}(y_0)\)，\(F(x, y) = 0\) 当且仅当\(y = \phi(x)\)； (iv) \(\phi(\cdot)\)是\(C^1\)的，且 [ D(x)=-.[D_yF(x, y)]^{-1}D_xF(x, y)|{y = (x)}, x B{}(x_0) ]

jacobian矩阵

题1

设\(F = (f, g): \mathbb{R}^4 \to \mathbb{R}^2\)， [ \[\begin{cases} f(x, y, u, v) = 3x^2 + y^2 + u^2 + v^2 - 1\\ g(x, y, u, v) = x^2 + 2y^2 - u^2 + v^2 - 1 \end{cases}\]

]

不难验证，点\(P_0 = (0, \frac{1}{2}, \frac{1}{\sqrt{8}}, \sqrt{\frac{5}{8}})\)是方程组\(F(x, y, u, v) = 0\)的一个解。考虑映射\(F\)在点\(P_0\)处的Jacobian矩阵 [ \[\begin{bmatrix} 6x & 2y & 2u & 2v\\ 2x & 4y & -2u & 2v \end{bmatrix}\] _{P_0}= \[\begin{bmatrix} 0 & 1 & \frac{1}{\sqrt{2}} & \sqrt{\frac{5}{2}}\\ 0 & 2 & -\frac{1}{\sqrt{2}} & \sqrt{\frac{5}{2}} \end{bmatrix}\]

]

由于矩阵 [ .D_{(u, v)}F|_{P_0}= \[\begin{bmatrix} \frac{1}{\sqrt{2}} & \sqrt{\frac{5}{2}}\\ -\frac{1}{\sqrt{2}} & \sqrt{\frac{5}{2}} \end{bmatrix}\]

]

注，其实这里\(\frac{\partial (f,g)}{\partial (u,v)}\),\(\frac{\partial (f,g)}{\partial (y,v)}\),\(\frac{\partial (f,g)}{\partial (y,u)}\)都非奇，我们取这个是为了把(x,y)映射到(u,v).

非奇，故由IFT（隐函数定理，Implicit Function Theorem）知存在\(C^1\)映射\(h: B_{\delta} \subset \mathbb{R}^2 \to \mathbb{R}^2\)，\((x, y) \mapsto (u, v) = (u(x, y), v(x, y))\)，使得

[ \[\begin{cases} u(x_0, y_0) = u_0\\ v(x_0, y_0) = v_0 \end{cases}\]

]

其中\(B_{\delta} = \{(x, y), (x - x_0)^2 + (y - y_0)^2 < \delta^2\}\)，且 [F(x, y, u(x, y), v(x, y)) , (x, y) B_{}]

进一步映射\(h\)在点\((x_0, y_0)\)处的Jacobian矩阵为 [ \[\begin{align*} \begin{bmatrix} u_x & u_y\\ v_x & v_y \end{bmatrix}_{(x_0,y_0)}&=-\begin{bmatrix} f_u & f_v\\ g_u & g_v \end{bmatrix}_{P_0}^{-1}\begin{bmatrix} f_x & f_y\\ g_x & g_y \end{bmatrix}_{P_0}\\ &=-\begin{bmatrix} \frac{1}{\sqrt{2}}&\sqrt{\frac{5}{2}}\\ \frac{-1}{\sqrt{2}}&\sqrt{\frac{5}{2}} \end{bmatrix}^{-1}\begin{bmatrix} 0&1\\ 0&2 \end{bmatrix}=\begin{bmatrix} 0&\frac{1}{\sqrt{2}}\\ 0&\frac{-3}{\sqrt{10}} \end{bmatrix} \end{align*}\] ]

注：这里可以进行联系二元情形的隐函数定理\(f'(x)=-\frac{F_x(x,y)}{F_y(x,y)}\)，分母对应y分子对应x。

题2

证明由方程组 \[ \begin{cases} x^{2}+y^{2}=\frac{1}{2}z^{2}\\ x + y+z = 2 \end{cases} \] 在点\((x,y,z)=(1, -1,2)\)附近，确定了两个隐函数\(x = x(z)\)，\(y = y(z)\)，\(z \in (2-\delta,2 + \delta)\)，满足\(x(2)=1\)，\(y(2)= -1\)，并且它们是\(C^{\infty}\)的。求\(x'(2)\)，\(y'(2)\)，\(x''(2)\)，\(y''(2)\)。

解：记\(F(x,y,z)=x^{2}+y^{2}-\frac{1}{2}z^{2}\)，\(G(x,y,z)=x + y+z - 2\)，则 \[ \begin{cases} F(1,-1,2)=0\\ G(1,-1,2)=0 \end{cases} \]

计算得 \[ \frac{\partial(F,G)}{\partial(x,y)}=\begin{bmatrix} 2x&2y\\ 1&1 \end{bmatrix} \] 由于 \[ \left.\frac{\partial(F,G)}{\partial(x,y)}\right|_{(1,-1,2)}=\begin{bmatrix} 2& -2\\ 1&1 \end{bmatrix} \] 非奇，故根据IFT知方程组 \[ \begin{cases} F(x,y,z)=0\\ G(x,y,z)=0 \end{cases} \] 注：关于某几个变量的Jacobian矩阵非奇，说明存在由其他的变量到这几个变量的映射。比如这道题就是z到x,y，即x(z),y(z)。上面的那一道题是x,y→u,v即u=(x,y),v=(x,y)。Jacobian矩阵非奇与偏导数不为零也有联系，比如我们想把z表示成关于x,y的函数，要求对z偏导数不为0，就是要求关于z的导数的jacobian矩阵（虽然只是一个元素）不为0 在点\((x,y,z)=(1, -1,2)\)附近，确定了两个隐函数\(x = x(z)\)，\(y = y(z)\)，满足\(x(2)=1\)，\(y(2)= -1\)。

由于函数 (F(x,y,z))，(G(x,y,z)) 是 (C^{}) 的，故隐函数 (x(z))，(y(z)) 也是 (C^{}) 的。以下求 (x^{}(2))，(y{}(2))。对恒等式

( \[\begin{cases} F(x(z),y(z),z) = 0 \\ G(x(z),y(z),z) = 0 \end{cases}\] ) 即 ( \[\begin{cases} x(z)^2 + y(z)^2 - \frac{1}{2}z^2 = 0 \\ x(z) + y(z) + z - 2 = 0 \end{cases}\]

)

求导得

( \[\begin{cases} 2x(z)x^{\prime}(z) + 2y(z)y^{\prime}(z) - z = 0, \\ x^{\prime}(z) + y^{\prime}(z) + 1 = 0. \end{cases}\]

)

令 (z = 2)，并注意到 (x(2) = 1)，(y(2) = -1) 得

( \[\begin{cases} 2x^{\prime}(2) - 2y^{\prime}(2) - 2 = 0, \\ x^{\prime}(2) + y^{\prime}(2) + 1 = 0. \end{cases}\]

)

易解得 (x^{}(2) = 0)，(y^{}(2) = -1)。为求 (x^{}(2))，(y{}(2))，我们需要对恒等式

( \[\begin{cases} 2x(z)x^{\prime}(z) + 2y(z)y^{\prime}(z) - z = 0, \\ x^{\prime}(z) + y^{\prime}(z) + 1 = 0, \end{cases}\]

)

再次求导得

( \[\begin{cases} 2x^{\prime}(z)^2 + 2x(z)x^{\prime\prime}(z) + 2y^{\prime}(z)^2 + 2y(z)y^{\prime\prime}(z) - 1 = 0, \\ x^{\prime\prime}(z) + y^{\prime\prime}(z) = 0. \end{cases}\]

)

令 (z = 2)，并注意 (x(2) = 1)，(y(2) = -1)，(x^{}(2) = 0)，(y^{}(2) = -1) 得

( \[\begin{cases} 2x^{\prime\prime}(2) + 2 - 2y^{\prime\prime}(2) - 1 = 0, \\ x^{\prime\prime}(z) + y^{\prime\prime}(z) = 0, \end{cases}\] ) 即 ( \[\begin{cases} x^{\prime\prime}(2) - y^{\prime\prime}(2) = -1/2, \\ x^{\prime\prime}(z) + y^{\prime\prime}(z) = 0. \end{cases}\]

)

易解得 (x^{}(2) = -)，(y^{}(2) = )。解答完毕。

逆映射定理

设\(f:\Omega\subset\mathbb{R}^n\to\mathbb{R}^n\)是\(C^1\)映射，\(\Omega\)开，\(x_0\in\Omega\)。若\(n\)阶Jacobian矩阵\(Df(x_0)\)非奇，则存在映射\(g:B_{\delta}(y_0)\subset\mathbb{R}^n\to\mathbb{R}^n(y_0 = f(x_0))\)使得 (i) \(x_0 = g(y_0)\)； (ii) \(f(g(y)) = y\)，\(y\in B_{\delta}(y_0)\)； (iii) \(g(f(x)) = x\)，\(\forall x\in B_{\varepsilon}(x_0)\)； (iv) 映射\(g(\cdot)\)是\(C^1\)的，且 [ Dg(y)=.[Df(x)]^{-1}|{x = g(y)}, yB{}(y_0) ]

例

极坐标变换为\(x = r\cos\theta\)，\(y = r\sin\theta\)，其Jacobian矩阵为 [ = \[\begin{bmatrix} \cos\theta & -r\sin\theta\\ \sin\theta & r\cos\theta \end{bmatrix}\]

]

易证极坐标变换在区域\(r > 0\)，\(0 < \theta < 2\pi\)上可逆，逆变换为\(r = \sqrt{x^2 + y^2}\)，\(\theta = \theta(x, y)\)的Jacobian矩阵为 [ =^{-1}= \[\begin{bmatrix} r\cos\theta & r\sin\theta\\ -\sin\theta & \cos\theta \end{bmatrix}\]

]

隐函数的高阶导数

隐函数的高阶导数计算

例：设三元函数\(F(x,y,z)\)在开集\(\Omega \subset \mathbb{R}^3\)上是\(C^1\)的。设\(P_0 = (x_0,y_0,z_0) \in \Omega\)，使得\(F(x_0,y_0,z_0) = 0\)且\(F_z(x_0,y_0,z_0) \neq 0\)。于是由IFT知可由方程\(F(x,y,z) = 0\)在点\(P_0\)附近解出唯一的隐函数\(z = z(x,y)\)，\((x,y) \in B_\delta\)，这里\(B_\delta\)表以点\((x_0,y_0)\)为心，以\(\delta > 0\)为半径的开球域。进一步函数\(z(x,y)\)的偏导数可表为 \[(z_x,z_y)|_{(x,y)} = -\frac{(F_x,F_y)}{F_z}|_{(x,y,z(x,y))}, \quad (x,y) \in B_\delta. \quad (*)\] 如之前所提及过的，隐函数\(z(x,y)\)的光滑性同函数\(F(x,y,z)\)。故当\(F\)是\(C^2\)时，隐函数\(z(x,y)\)也是\(C^2\)的。以下以计算二阶偏导数\(z_{xx}\)为例，来说明如何计算隐函数的高阶偏导数。由导数公式知\(z_x = -F_x/F_z\)。于是

\[ \begin{align*} z_{xx} &= -\left[\frac{F_x(x,y,z(x,y))}{F_z(x,y,z(x,y))}\right]_x = -\frac{1}{F_z^2}[F_z(F_x)_x - F_x(F_z)_x]\\ &= -\frac{1}{F_z^2}[F_z(F_{xx} + F_{xz}z_x) - F_x(F_{zx} + F_{zz}z_x)]\\ &= -\frac{1}{F_z^2}\left[F_z\left(F_{xx} + F_{xz}\left[-\frac{F_x}{F_z}\right]\right) - F_x\left(F_{zx} + F_{zz}\left[-\frac{F_x}{F_z}\right]\right)\right]\\ &= \frac{1}{F_z^3}\left(2F_xF_zF_{xz} - F_z^2F_{xx} - F_x^2F_{zz}\right)\Bigg|_{(x,y,z(x,y))} \end{align*} \] 类似可求其他两个二阶偏导数\(z_{xy}\)，\(z_{yy}\)。